基于量纲分析从物理和数学角度推导光速原理-凯发国际一触即发

基于量纲分析从物理和数学角度推导光速原理
derivation of the principle of light speed from physical and mathematical perspectives based on dimensional analysis

doi: , , , ,
作者: ：昆明物理研究所，云南昆明
关键词: ；；；；；；；；；；；；；

摘要: 介绍了量纲关系“能量 ≡ 质量×(速度)2”的推导过程，讨论了质量体的概念。分别从物理和数学角度推导了光速原理，即宇宙总能量和宇宙总质量比值的平方根等于光速。光子是以光速运动的质量体。讨论了引力对于光速的影响。在没有引力或者引力作用的影响可以忽略的条件下光速不变。

abstract: the deduction process of dimensional relation of “energy ≡ mass × (speed)2” is introduced. the concept of mass body is discussed. the principle of light speed is deduced respectively from the physical and mathematical point of view, that is, the square root of the ratio of the total universal energy to the total universal mass equals light speed. photons are mass bodies moving at light speed. the effect of gravitation on light speed is discussed. the light speed remains unchanged in cases where there is no gravitation or the effects of gravitation are negligible.

文章引用：王忆锋. 基于量纲分析从物理和数学角度推导光速原理[j]. 现代物理, 2019, 9(4): 183-190.

1. 引言

量纲分析(dimensional analysis)是通过分析问题所涉及物理量的属性来建立因果关系的方法 [1] 。通过量纲分析可以判断事物间数量关系所遵循的一般规律，甚至有可能提供理解或者寻找某些物理现象内在规律的线索。本文在作者已有工作的基础上 [2] - [14] ，介绍了量纲关系“能量 ≡ 质量 × (速度)²”的分析推导过程，讨论了质量体的概念，在此基础上分别从物理和数学的角度介绍了两种新的导出光速原理的简单方法。

2. 基本量纲关系

物理量的基本属性称为量纲，它们是物理量的度量单位。在物理学的国际单位制中，将量纲分为基本单位、导出单位和辅助单位。其中基本单位包括质量(千克，kg)、长度(米，m)、时间(秒，s)、电流(安培，a)、热力学温度(开尔文，k)、物质的量(摩尔，mol)和发光强度(坎德拉，cd)等七个物理量。

相同的物理量纲可以构成等价关系，例如

$质量 \equiv 质量$ ， $长度 \equiv 长度$ (1)

这里用“≡”表示量纲意义上的等价关系。量纲相同不一定量值相等。本文用符号“=”表示量值或者数值意义上的等量关系。

不相同的物理量纲不能构成等价或者等量关系，因此有“≠”关系。例如

$质量 \neq 长度$ (2)

量纲相同的物理量可以执行加减乘除等代数运算；量纲不相同的物理量之间不能加减，只能相乘或者相除。

由于物理学的国际单位制中的七个基本量纲不足以满足使用要求，因此需要以基本量纲为基础来定义新量纲。例如，速度等于长度除以时间，

$速度 \equiv \frac{长度}{时间}$ (3)

长度的三次方定义为体积，

$体积 \equiv 长度 \times 长度 \times 长度$ (4)

质量除以体积定义为密度，

$密度 \equiv \frac{质量}{体积}$ (5)

3. 量纲关系“能量 ≡ 质量 × (速度)²”的推导过程

因为质量和速度分别属于不同的量纲，故有

$质量 \neq 速度$ (6)

假设再定义一个新量纲δ，相应有

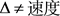(7)

将不等式(6)和不等式(7)两边相乘可得

$质量 \times δ \neq (速度) \times (速度) = {(速度)}^{2}$ (8)

现在考虑这样一个问题：质量、新量纲δ和速度三个物理量，与加减乘除等代数运算法则任意组合，能否“拼凑”出一个等式关系？具体地说，该等式以不等式(8)的构形为基础，左边由质量和δ两项组合而成，右边仍然是(速度)²。

下面分析这一问题。因为加法、减法不可以直接用于不同物理量的运算，所以“ ”、“−”被排除；根据乘法交换律，两个量a和b之间乘法关系只有一种，即a × b = b × a；另外在不等式(8)中已经用了乘法，所以只剩下除法可供选用。a和b之间的除法关系有两种，可以是a/b，也可以是b/a；故基于除法组合的等式关系有

$\frac{δ}{质量} \equiv {(速度)}^{2}$ (9)

或者

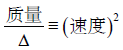(10)

除此之外，再也没有其他可能的组合选项。

式(9)两端乘以质量，可得

$δ \equiv 质量 \times {(速度)}^{2}$ (11)

从因果关系的角度来看式(11)，就是δ为结果，引起δ变化的原因可以是速度、也可以是质量；从函数的角度来看，就是量纲δ是质量和速度的函数，δ与质量成正比、还与速度的平方成正比。

类似地，式(10)两端乘以δ，可得

$质量 \equiv δ \times {(速度)}^{2}$ (12)

从因果关系的角度来看式(12)，就是质量为结果，引起质量变化的原因可以是速度、也可以是δ。从函数的角度来看，就是质量是量纲δ和速度的函数，质量与δ成正比、还与速度的平方成正比。

式(11)和式(12)是两种截然不同的物理观。这是一个二选一的问题，如果认可质量是速度的函数则选式(12)，反之就要选式(11)。

事实上，看一看现今能量量纲焦耳(j)的定义

$1 j = 1 kg \cdot {(m / s)}^{2}$ (13)

可以发现焦耳(j)的定义在量纲上与式(11)相同，即前面分析的新量纲δ就是能量的量纲，将式(11)中的δ换成“能量”，则有

$能量 \equiv 质量 \times {(速度)}^{2}$ (14)

4. 概念的符号化

数学化是现代科学的特点之一。数学化首先是概念的符号化。例如，将长度记为l，将时间记为t，将速度记为u，则有

$速度 \equiv \frac{长度}{时间} \Rightarrow u \equiv \frac{l}{t}$ (15)

目前已知最快的速度是光速 $c (= 2.998 \times 10^{8} m / s)$ 。换言之，速度u可以在0~c之间任意取值。由于0~c之间的量值跨度范围非常大，为了简化讨论，本文将速度u分为u = 0 (静止)、u < c (非光速)和u = c (光速)三类。

另外，将质量记为m，将能量记为e，则有

$能量 \equiv 质量 \times {(速度)}^{2} \Rightarrow e \equiv m u^{2}$ (16)

将体积记为v，将密度记为d，则有

$密度 \equiv \frac{质量}{体积} \Rightarrow d \equiv \frac{m}{v}$ (17)

5. 关于质量体的概念

思维是对事物的间接反映。概念是思维的基本单位。任何一个学科体系总是要对概念下定义。由于概念的个数是有限的，因此总有一些概念不能引用别的概念来定义，这样的概念就是原始概念。物理学国际单位制中的质量、长度和时间等七个基本单位即属于典型的原始概念。定义新概念的一种方法是基于原始概念的组合来衍生新概念，如上节所示。

定义新概念的另一种方法是将若干已知的、含义相近的概念归并在一起，以它们的共同点为基础提炼产生新概念。例如，综合考察物质、物体和质点这三个概念，可以看到质量是它们的共同点。基于这样一个共同点，作者提出了质量体(mass body)的概念 [13] [14] 。

顾名思义，质量体是“质量”与“体”这两个概念的组合。“质量”必定以“体”的形式存在。因为“质量”可以大也可以小，“体”同样可以大也可以小，两者可以构成不同的变化组合。例如：

1) 只考虑质量m、不考虑体积v时，就是质点的概念。牛顿万有引力定律“任意两个质点有通过连心线方向上的力相互吸引”，用的就是质点的概念；

2) 质量微小的质点称为微粒。如果把振动物体视为不考虑体积的微粒，这个振动物体就叫谐振子；

3) 质量m→有限、体积v→有限，就是通常意义上的物体概念；

4) 密度m/v→∞，这就是所谓黑洞的概念。从这个定义式(17)可以看出，质量的变化以及体积的变化均有可能导致密度的变化满足黑洞的概念。

上述有关质量体概念细分的讨论可以如所示。质量体包括了物质、物体和质点等概念的内涵，可以作为一个从微观到宏观均适用的原始概念。

6. 推导光速原理的两种新方法

作者在文献 [2] 中探讨了光子的可分裂性，在文献 [3] [4] [5] 中提出了可分裂的光子模型。在文献 [6] [7] [8] [9] [10] 探讨了光子分裂模型的若干应用问题，指出宇宙总能量和宇宙总质量比值的平方根等于光速 [6] [7] [8] [9] ，这一结果称为光速原理 [11] [12] 。文献 [13] [14] 对光速原理进行了深入探讨和分析。在这些工作和思考的基础上，作者形成了两种更为简单的推导光速原理方法，现介绍如下。

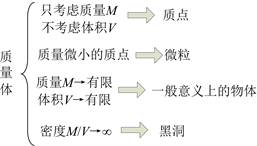
. subdivision of the concept of mass body

. 质量体概念的细分

6.1. 基于物理角度推导光速原理

众所周知，惯性是物体或者质量体保持原来运动状态不变的性质，它是一切质量体都具有的性质。当一个较小的质量体从一个较大的质量体中分离或者分裂时，由于惯性，在分裂瞬间较小的质量体的运动速度和较大的质量体的运动速度相同。

例如，设有一个质量体m_u，其运动速度为u_u。假设在某一时刻，m_u分裂为m₁和m₂；由于惯性，在分裂的瞬间，m₁、m₂的运动速度与m_u的运动速度相同、均为u_u；由于分裂，质量体的个数由原来的一个变成了两个，原来的质量体m_u不复存在，但是在总量关系上有

$m_{u} = m_{1} m_{2}$ (18)

在式(18)两端乘以速度的平方 $u_{u}^{2}$ ，则有

$m_{u} u_{u}^{2} = (m_{1} m_{2}) u_{u}^{2}$ (19)

根据上节讨论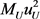，具有能量的量纲。

将上述讨论推广到m_u分裂为无穷多个质量体的情况，则有

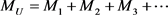(20)

宇宙由无穷多个质量体构成，所以式(20)可以视为宇宙体系的质量模型，其中m_u为宇宙总质量。在认可质量守恒的前提下，宇宙总质量m_u是一个不变量，或者说是一个无穷大的常数。

类似地由于惯性，在m_u分裂的瞬间， $m_{1}, m_{2}, m_{3}, \dots$ 的运动速度和m_u的运动速度相同、均为u_u。在式(20)两端乘以，可得

$m_{u} u_{u}^{2} = (m_{1} m_{2} m_{3} \dots) u_{u}^{2}$ (21)

在式(21)中，因为m_u为宇宙总质量，该式具有能量的量纲，因此很自然地就会提出宇宙总能量(e_u)是多少的问题。

从概念上说，速度u_u可以在0~c之间任意取值。因为物质或质量体是运动的，没有不运动的质量体，所以u_u= 0的选项被排除；如果u_u< c，从常识知道，一个质量体的总能量未必是其质量和运动速度平方的乘积，换言之，当u_u≠ c时，一个质量体的总能量与其质量和运动速度三者之间的关系是不确定的，另一方面，一个质量体必然有一个总能量，于是只有u_u= c一种选项，相应地宇宙总能量e_u为

$m_{u} c^{2} = e_{u}$ (22)

在m_u为常数的前提下，因为光速c是运动速度的最大值，故 $m_{u} c^{2}$ 也是最大值，此时三者之间的关系是确定的，具有唯一性。因此u_u= c是最合适的选项。

6.2.基于数学角度推导光速原理

在数学上我们知道，在满足总和为1的前提下，1可以分解为无穷多个正小数或者正分数之和，例如

$1 = 0.1 0.01 0.001 \dots$

一般形式可以写为

$1 = \sum_{i = 1}^{\infty} a_{i}, 0 < a_{i} < 1$ (23)

在式(23)两端乘以一个无穷大的正常数m_u，则有

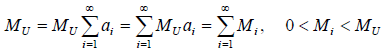(24)

或者

$m_{u} = m_{1} m_{2} m_{3} \dots$ (25)

式(23)没有物理量纲，它从数学上描述了一种整体可以无限分解为局部的思想，同时“1”意味着不变，意味着守恒。如果m_u具有特定的量纲，则式(24)可能就具有一定的物理意义。这里取m_u表示宇宙总质量，则式(25)表示宇宙总质量m_u为宇宙中所有质量体的质量之和，它还意味着宇宙中的所有质量体源于一个(总的)质量体的分裂。

另一方面，物质或者质量体是运动的，没有不运动的物质或者质量体。如果认同这一观点，则意味着宇宙中的每一个质量体都有一个运动速度，假设质量体 $m_{1}, m_{2}, m_{3}, \dots$ 的运动速度分别为 $u_{1}, u_{2}, u_{3}, \dots$ ；同样，总的质量体m_u也有一个运动速度u_u。

从数学上说，一般情况下有

$m_{u} u_{u}^{2} \neq m_{1} u_{1}^{2} m_{2} u_{2}^{2} m_{3} u_{3}^{2} \dots$ (26)

式(26)两端均为能量的量纲。当且仅当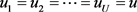、即速度全同时，式(26)中的不等号变为等号，即

$m_{u} u^{2} = m_{1} u^{2} m_{2} u^{2} m_{3} u^{2} \dots = (m_{1} m_{2} m_{3} \dots) u^{2}$ (27)

也就是说所有质量体的运动速度必须相同，式(27)才成立；否则，只要有一个质量体的运动速度不同，式(27)即不成立。

本来当质量体 $m_{1}, m_{2}, m_{3}, \dots$ 出现时，总的质量体m_u已经不存在；但是如果要使式(27)成立，则要求质量体 $m_{1}, m_{2}, m_{3}, \dots$ 与总的质量体m_u同时存在；在什么情况下满足同时存在的要求？可以认为在总的质量体m_u分裂为 $m_{1}, m_{2}, m_{3}, \dots$ 的那一瞬间它们同时存在，并且由于惯性，它们的运动速度相同，这意味着要把时间的尺度拉回到宇宙诞生的初始时刻。这一点还可以从引力的角度来分析。牛顿提出的万有引力定律指出：任意两个质点有通过连心线方向上的力相互吸引。这里的前提条件是“两个质点”；m_u为一个质点的情况，因其不满足万有引力定律的适用条件，故此时没有引力。当m_u分裂成 $m_{1}, m_{2}, m_{3}, \dots$ 等较小的质量体时，一方面， $m_{1}, m_{2}, m_{3}, \dots$ 的初始运动速度与m_u的运动速度相同，另一方面，因为分裂之后质量体的数量大于二，满足万有引力定律的适用条件，随之出现的引力作用必然使得若干质量体的运动速度发生变化，导致速度全同的条件不再满足；换言之，式(27)的成立隐含着对特定时间点的严格要求。

从计算的角度上看，运动速度u的任何取值均可让式(27)成立。但是如果u < c，将无法解释光速c从何而来的问题，所以最合理的选择是u = c。于是有

$m_{u} c^{2} = (m_{1} m_{2} m_{3} \dots) c^{2} = e_{u}$ (28)

式中，e_u为宇宙总能量，这个结果与式(22)相同。

从式(28)可以写出

$\frac{e_{u}}{m_{u}} = c^{2} \Rightarrow \sqrt{\frac{e_{u}}{m_{u}}} = c$ (29)

即宇宙总能量和宇宙总质量比值的平方根等于光速，这是作者提出的光速原理。作者曾以很多篇幅来分析论证，这里给出了两种比较简单的推导方法。

光速原理成立的前提是速度全同，即每一个分裂出来的质量体均以光速运动(以光速运动的质量体称为光子)，于是有

$e_{i} = m_{i} c^{2}$ (30)

不失一般性，将式(30)中的下标i去掉，可以写出

$e = m c^{2}$ (31)

式(31)称为光子的质量-能量关系式，在狭义相对论中称为质能方程。可以注意到，这里的分析过程与相对论没有任何关系。

式(31)是一个光子能量的计算公式；事实上还有一个光子能量的计算公式，这就是爱因斯坦提出的光(量)子能量模型

(32)

式中， $h (= 6.626 \times 10^{- 34} j \cdot s)$ 为普朗克常数，为波长。表面上看，式(32)中没有包含光子的质量，但是因为普朗克常数中有焦耳(j)，而焦耳(j)的定义中包括质量的量纲，所以实际上式(32)隐含地与质量相关；换言之，式(32)与式(31)在量纲上并不矛盾。

在认同式(31)和(32)正确性的前提下，联立它们可以求出光子质量为

(33)

应该指出一点：光子有没有质量与是否可以测量出光子的质量是两个不同的概念。从过程的角度来看，人类目前感知到的光子没有质量并不意味着过去的光子没有质量，也并不意味着未来的光子没有质量。

20世纪初，数学家埃米·诺特提出了诺特定理，该定理指出对于力学体系的每一个连续的对称变换，都有一个守恒量与之对应。宇宙中的所有质量体构成一个最大的力学体系。根据诺特定理，宇宙的总能量和总动量肯定是守恒的，但是诺特定理并没有告诉我们如何计算，也没有指出守恒量具体为多少。光速原理给出了这些问题的答案。因为宇宙总质量m_u守恒、光速c为常数，故式(28)表示的宇宙总能量 $e_{u} = m_{u} c^{2}$ 守恒。类似地，m_uc同样守恒；m_uc具有动量的量纲，它表示宇宙总动量的守恒。这些结果都是满足诺特定理的。

从逻辑上说，如果认可诺特定理是正确的、普适的，因为光速原理给出的结果满足诺特定理的要求，那么光速原理也可以被认为是正确的。

7. 结束语

光速原理指出宇宙总能量和宇宙总质量比值的平方根等于光速。光速是质量体运动速度的极限，这意味着作为速度最大值的光速是恒定不变的，这是从数值角度而言。外力可以影响质量体的运动速度，这一点对于以光速运动的质量体来说也不例外，所以光速又是可变的，这是从质量体运动特性变化的角度而言。

外力对质量体运动特性的影响可以简单地分为加速作用和减速作用。在各种形式的外力中，最为典型、影响最大的外力是引力。对于以光速运动的质量体而言，加速作用弱时其影响可以忽略不计，质量体还是以光速运动；加速作用强时又将导致质量体分裂(光子分裂)，不可能从光速变为超光速，或者说最终维持在光速。

根据牛顿万有引力定律，只要有两个质量体就有引力存在。当只有一个质量体时，不符合万有引力定律的条件，此时没有引力；什么情况下才可能有一个质量体？这就是宇宙之始，此时该质量体以光速运动，这就是光速的起源；什么时候引力作用可以忽略不计？质量特别小的质量体感受到的引力可以忽略不计，人类目前感知的光子即属于质量特别小的质量体，所以一般情况下光子的运动速度不会改变，除非对光子产生引力的质量体特别巨大，例如黑洞。这些情况归纳起来就是：在没有引力或者引力作用可以忽略的条件下光速不变。

在表现为减速作用的引力影响下，一方面，质量体的运动速度从高速降到低速，另一方面，质量体的运动轨迹也会发生相应的改变。光子的运动轨迹为直线。对于质量足够小的光子，如果引力不够大，光子还是以直线前进；当引力足够大时，对于质量足够小的光子的运动轨迹也有影响；这一点从表面上是引力足够大，但本质上是产生引力的质量体足够大，这就是为什么在太阳附近可以观察到光线偏折了若干度，而在地球附近观察不到光线的偏折；如果引力足够大，例如在黑洞附近，引力将使更多的光线偏折(在几何光学中使光线偏折的器件称为透镜)，从而形成引力透镜现象。

参考文献

[1]	谈庆明. 量纲分析[m]. 合肥: 中国科技大学出版社, 2005: 1-3.
[2]	王忆锋, 黄江平. 试论光子的分裂[j]. 红外, 2014, 35(3): 1-6.
[3]	王忆锋. 论可分裂的光子模型[j]. 云光技术, 2015, 47(1): 1-17.
[4]	王忆锋. 关于可分裂的光子模型的进一步分析和探讨(上) [j]. 红外, 2016, 37(13): 1-5.
[5]	王忆锋. 关于可分裂的光子模型的进一步分析和探讨(下) [j]. 红外, 2016, 37(14): 10-12, 18.
[6]	王忆锋. 论光子分裂视角下的宇宙观(上) [j]. 红外, 2017, 38(3): 1-5.
[7]	王忆锋. 论光子分裂视角下的宇宙观(中) [j]. 红外, 2017, 38(1): 6-11.
[8]	王忆锋. 论光子分裂视角下的宇宙观(下) [j]. 红外, 2017, 38(3): 44-48.
[9]	王忆锋. 论超光速量子纠缠的不可能性[j]. 云光技术, 2016, 48(1): 52.
[10]	王忆锋. 论光子分裂视角下二进制数据的量子态表达[j]. 红外, 2017, 38(12): 7-12, 30.
[11]	王忆锋. 论以光速原理为标志的第三次科学革命[j]. 云光技术, 2017, 49(1): 1-10.
[12]	王忆锋. 论麦克斯韦方程组对于描述光子辐射的不适用性与基于电荷数差值的光电信号转换模型[j]. 云光技术, 2017, 49(1): 41-53.
[13]	王忆锋. 论光子本性的公理化逻辑分析[j]. 云光技术, 2017, 49(2): 41-65.
[14]	王忆锋. 论若干物理问题的量纲分析方法[j]. 云光技术, 2018, 50(1): 42-51.

为你推荐

凯发国际一触即发的友情链接