1. 引言
主效应因素分析广泛应用于故障诊断、事故分析、风险分析等领域 [1] [2],能够为事故原因定位、致因分析以及制定有效预防措施提供定性定量分析依据。贝叶斯网络作为一种结合数据挖掘和不确定性知识推理的人工智能技术,已经广泛应用于各个领域,其优势之处主要体现在能够通过有向无环图表达出节点之间的相互关系,通过节点之间的条件概率进行不确定性知识推理 [3]。基于贝叶斯网络的致因分析方法,通常包括因素提取、贝叶斯网络结构构建、贝叶斯网络参数计算、直接影响因素定位、灵敏度分析与排序等步骤,最后将灵敏度最高的直接影响因素作为导致事故发生的主效应因素。
现有基于贝叶斯网络的主效应因素分析方法多数基于构建的贝叶斯网络结构对影响事故发生的因素进行单独的灵敏度分析,从而实现致因定位或者故障定位。这种方法虽然在贝叶斯网络结构构建时考虑了因素之间的关联关系,在因素灵敏度分析时却忽略了因素之间的交互效应,有可能导致片面的分析结论,从而影响致因分析的全面性和可信度。
如果一个因素不仅直接对结果节点产生影响,同时通过影响另一个因素进而对结果节点产生影响,那么我们认为这两个因素之间是存在交互效应的,在因素对结果影响分析的时候,除了要考虑因素本身对结果节点的直接影响,必须分析因素对交互效应的节点的影响,进而形成全面的分析结论。基于此,本文提出一种基于贝叶斯网络的主效应因素分析方法,在充分利用因素之间的关联关系进行贝叶斯网络结构构建之后,分析各因素的影响路径并进行灵敏度分析和致因分析。这种方法不是简单割裂地对各因素进行单独分析,而是充分考虑因素之间的交互效应,从而得到更加可靠全面的致因分析结论。
2. 相关工作
随着国内外学者对主效应分析理论的不断研究和发展,学术界提出了多种分析模型,包括因果连锁模型、轨迹交叉模型、瑟利模型、突变模型等 [4]。主效应因素分析方法的发展趋势是多种因素协同分析,单一因素分析方法不能满足现阶段复杂过程的诊断分析需求。隶属于机器学习算法的贝叶斯网络作为一种可以融合多源信息的不确定性知识表迖与推理模型,在数据学习的基础上能与专家知识等多种方法进行有效结合,协同诊断。其优势体现在 [5]:1) 基于图模型,能贴切并直观地描述变量间的因果关系和条件相关性;2) 具备基于数学概率理论的不确定性推理能力,能在有限的、不完整的信息条件下进行学习、推理和更新;3) 能有效融合和表达多源信息。因此,基于贝叶斯网络的主效应分析方法适合于表达复杂过程中错综复杂的因果关系。其在信息的表达能力、不确定条件下的学习能力、与其他方法的结合能力、模型更新能力、多源信息融合处理能力以及解释性等方面的综合性能比神经网络、故障树等其他智能算法更适用于主效应因素分析问题 [6] [7] [8]。
文献 [9] 将贝叶斯网络作为一种事故分析手段,提出了一种基于危险因素–事故–事故危害的三层贝叶斯网络拓扑模型,更加全面地分析事故的致因因素以及其可能导致的各种后果,同时实现对事故类型和事故后果的预测。文献 [10] 基于贝叶斯网络模型,综合运用诊断推理和支持推理形式,分析致灾因素的因果关系,揭示了人、机、环境与管理因素相互作用的内在规律,对事故致因因素进行了更深入的挖掘,有助于及时发现系统中潜在的事故隐患。文献 [11] 提出了一种基于贝叶斯网络模型理论的交通事故预测方法。在综合考虑交通事故成因的基础上利用领域专家知识构建网络模型,在已有的事故数据的基础上提出基于贝叶斯法则的学习算法,并通过计算变量间的条件概率来计算事故发生的可能性,达到事故预测的目的。文献 [12] 通过建立基于事故样本数据的贝叶斯网络模型,将贝叶斯网络应用于道路交通事故原因推理中。该模型特点是综合了驾驶员、道路状况、天气等多方面因素,但同时也存在一定的不足,即对这些因素难以进行有效的量化。文献 [13] 利用贝叶斯网络对铁路事故进行致因分析,在融合领域知识和样本数据的基础上建立贝叶斯网络。文献 [14] 结合人为组织因素应用贝叶斯网络进行风险分析,利用贝叶斯网络的推理能力,对海上运输系统内的人为组织因素,包括船公司、港口管理、规章制度等,进行了风险分析。文献 [15] 基于前人所建的网络结构,进一步确定了船舶碰撞的致因因素,并确定出贝叶斯网络结构,利用软件对船舶碰撞事故的发生概率进行了预测分析。
上述文献表明,贝叶斯网络可以从定量的角度进行主效应因素分析,其自身具有的推理功能可以成为主效应因素分析的有效工具。然而上述方法的缺陷在于缺乏对因素间交互效应的考虑,影响了分析结论的客观可行程度。本文算法的核心思想在于交互效应分析。在构建贝叶斯网络模型后,首先对利用网络结构连接关系,定位对结果节点产生直接影响的因素作为直接影响因素,然后考虑到这些因素之间可能存在着交互效应,分析每个直接影响因素对结果节点的影响路径,形成因素对结果的影响节点集合。再从影响节点集合中筛选受直接影响因素影响较大的节点作为交互效应节点,最后利用直接影响因素和对应的交互效应节点联合分析其对结果节点的影响程度,作为直接影响因素的影响度。影响度最大的直接影响因素就是所要寻找的主效应因素,对待分析样本的发生起到至关重要的作用。
3. 主效应因素分析流程
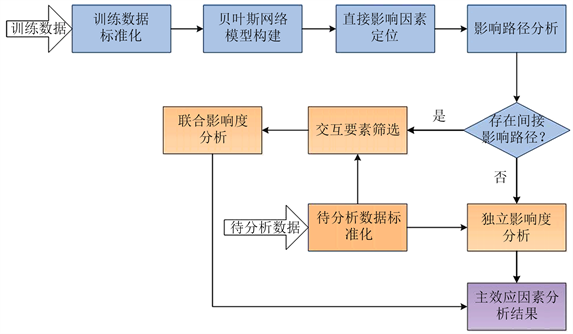
本文算法流程如所示,主要包括数据标准化、建立贝叶斯网络模型、直接影响因素定位、影响路径分析、独立影响度分析、联合影响度分析等六个关键步骤。其中灰色框中的步骤是训练分析阶段进行的,输入为训练数据,输出为影响路径分析结果。橙色框中的步骤是主效应因素分析阶段进行的,输入为待分析数据,输出为主效应因素分析结果。详述如下:
3.1. 训练数据标准化
训练数据标准化主要是将原始数据转换为用于主效应因素分析的离散化标准数据。记用于贝叶斯网络构建训练的原始数据集为
,n表示训练样本数量,第i个样本
,
表示
的第j个特征,m表示训练样本特征的维数,
表示第i个样本对应的事故发生情况,若发生为1,未发生为0。对于离散型特征和连续型特征采取不同的标准化方法。
. the main effect factor analysis process proposed in this paper
. 本文提出的主效应因素分析方法流程
假设第j个特征为离散型特征,即该特征取值个数为确定的有限正整数k,为了简化计算,需将所有样本中该特征的取值规范化到
这个集合范围内。首先对该特征的k个不同取值进行从小到大排序处理,得到排序后的指标取值集合。规范化后的特征
,k表示
在排序后的指标取值集合中的序号。
假设第j个特征为连续型特征,则需要进行离散化处理。采用二值化离散方法,首先求该特征的均值为:
(1)
离散化后的特征为:
(2)
至此,完成了训练数据标准化。
3.2. 建立贝叶斯网络模型
标准化后的训练数据集记为
。基于标准化后的数据集
,采用bic评分 爬山法构建贝叶斯网络结构。在贝叶斯网络中,每个节点对应于样本的一维特征,所有样本特征构成一个包含
个节点的网络结构。所有可能的网络结构构成了网络结构空间g,贝叶斯网络结构空间中的点g是一个
的二值矩阵,
为1表示存在一条节点i指向节点j的有向边。bic评分的计算公式如下:
(3)
其中g表示网络结构,d表示训练数据集,
表示网络结构g的bic评分,
表示第i个节点,
表示
可能的取值个数,
表示
的父节点取值的组合数。
表示
取第k个值,
的父节点取值为第j个组合的样本个数,
表示
的父节点取值为第j个组合的样本个数。
建立贝叶斯网络,首先随机生成网络空间g 中的一个点
作为爬山搜索的起点,并计算
的bic评分
。接着对
进行随机局部操作,随机局部操作类型包括加边、减边、转边三种,得到随机操作后的网络结构
,并计算
的bic评分
。如果
,则认为
比
更优,令
。重复进行局部随机操作与评分比较,直到达到迭代次数。
至此,确定了贝叶斯网络结构中节点之间的连接关系,用矩阵
表示。接着利用数据集
统计计算网络中各节点的条件概率表。例如计算节点i的条件概率,首先要确定节点i的父节点结合
,然后统计
不同取值组合情况下节点i取不同值的次数,计算
的值作为该节点的条件概率。
3.3. 直接影响因素定位
假设节点
为表示事故发生情况的结果节点,那么根据贝叶斯网络结构
可以确定结果节点的父节点集合
。在
中有一部分节点与结果节点之间存在直接的因果关系,这部分节点的序号构成集合记为
,满足
,
就是我们要确定的直接影响因素集合。
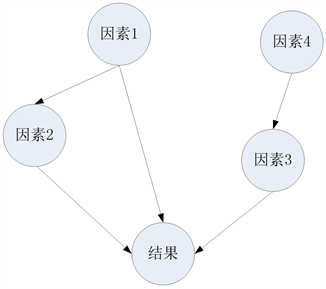
中还有一部分节点通过其他节点对结果节点产生影响,成为间接影响因素节点。例如的贝叶斯网络结构模型中,因素1、因素2、因素3都是与结果节点有直接连接关系的节点,因此是结果的直接影响因素。
. examples of direct influencing factors positioning
. 直接影响因素定位示例
3.4. 影响路径分析
直接影响因素集合
中的每个特征对应的特征节点与结果节点之间必然存在直接的连接,这种直接的连接对应于因素对结果的直接影响路径。除此之外,直接影响因素还有可能通过其他的因素对结果产生影响,例如节点
可能通过若干个间接影响因素和另外一个直接影响因素
对结果产生间接影响,这些间接影响因素和另一个直接影响因素就构成了节点
到结果节点的间接影响路径。遍历矩阵
,寻找每个直接影响因素节点对结果节点的影响路径集合。记节点
的影响路径集合为
,其中
表示节点
到结果节点的直接影响路径,
表示间接影响路径的总数,
表示节点
到结果节点的n条间接影响路径,假定第j条间接影响路径为
,包含
个节点,那么
必然对结果节点有直接影响,贝叶斯网络结构中存在一条从节点
到结果节点的连接。如果
中只包含一条直接影响路径
,那么直接进行独立影响度分析,得到诸因素分析结论。如果存在间接影响路径,那么进行联合影响度分析,得到主效应因素分析结果。
例如的贝叶斯网络结构模型中,三个直接影响因素中,因素2对结果节点的影响路径只有一条直接影响路径,只需要进行独立影响度分析即可,而因素1对结果节点的影响路径除了直接影响路径之外,还有“因素1- > 因素2- > 结果”这条间接影响路径。这就是说因素1对结果节点的影响还可能通过影响因素2而间接影响结果,后续主效应因素分析需要考虑与因素2的交互效应,进行联合影响度分析。
3.5. 待分析数据标准化
取待分析的数据样本按照3.1训练数据标准化的方法进行标准化,标准化后的样本记为x。主效应因素分析主要是分析对样本x影响最大的特征因素。
3.6. 独立影响度分析
独立影响度分析即是分析直接影响因素集合
中每个因素对结果的影响程度。针对
中的任意一个因素
,构造样本
,满足除结果因素
以外的所有特征取值与x一致,将
输入贝叶斯网络模型,计算结果因素取值与x一致的概率记为
。随机改变
中因素
的取值,重新输入贝叶斯网络模型,计算结果因素取值与x一致的概率记为
。那么,因素
对结果节点的影响度为
。对
中所有因素分别计算其对结果节点的影响度,并选择影响度最大的因素作为主效应因素分析结果。
3.7. 联合影响度分析
影响路径集合
中所有节点构成了一个影响路径的节点集合
,包括直接影响因素节点
、间接影响节点
、结果节点
,l表示节点
和结果节点
之间的间接影响节点的个数。构造样本
,满足
集合以外的所有特征取
值与x一致,其余特征取值不定。
3.7.1. 交互因素筛选
首先通过计算节点
对节点
的影响,筛选与节点
有交互效应的节点。设定
的特征
取值为x中的特征
的值,输入构建好的贝叶斯网络结构中,计算节点
取值为x中特征
的值的概率,记为
。随机改变
的特征
的取值,计算节点
取值为x中特征
的值的概率,记为
。若
,则认为节点特征
的改变不会影响节点
的取值,反之认为节点特征
的改变会影响节点
的取值,因而会对结果节点的取值产生交互效应。
为交互效应判定阈值,θ取值越大,交互因素筛选要求越高,则要求因素之间具有很强的交互相关性,才作为交互效应因素,进行联合影响度分析,极端情况下取值为1,则趋同于独立影响度分析。θ取值越小,交互因素筛选要求越低,这时候考虑交互因素的比较全面,但是也会形成冗余的结论。因此本文实验中取值0.3,兼顾独立性和交互性要求。
3.7.2. 联合影响度分析
选择
中与
有没有交互效应的节点,将
中相应节点特征取值为x中相应的特征值,当前
中取值待定的特征包括节点
、与节点
有交互效应的节点、结果节点
。设定
的特征
取值为x中的特征
的值,输入构建好的贝叶斯网络结构中,计算结果节点
取值为x中结果节点取值的概率记为
。随机改变
的特征
的取值,重新输入构建好的贝叶斯网络结构中,计算结果节点
取值为x中结果节点取值的概率记为
。记特征
对结果节点的影响度为
。
对直接影响因素集合
中的每个因素计算其对结果节点的影响度,并选择影响度最大的节点作为影响待分析样本的主效应因素。
4. 实验验证
4.1. 数据描述
威斯康辛州乳腺癌(breastcancer)数据集是sklearn.datasets的内置数据集,包含了威斯康辛州记录的569个病人的乳腺癌恶性/良性(1/0)类别型数据(训练目标),以及与之对应的30个维度的生理指标数据。
4.2. 实验流程
在window10系统上使用python3.7实现本文所提出的算法,并使用breastcancer数据集对本文算法进行实验验证。利用原始数据集中包含的[569 × 30]维生理指标数据和对应的569个类别型数据构成569个31维的训练样本数据。其中除类别型数据外,其他生理指标数据均为连续型特征,需要利用公式(1)计算各自特征离散化阈值并安装公式(2)进行特征离散化,得到标准化后的训练样本数据。之后利用爬山算法构建贝叶斯网络结构模型,该模型中类别型数据对应的节点作为结果节点,定位直接影响因素、分析影响路径。输入待测样本进行影响度分析。
4.3. 实验结果
构建的贝叶斯网络模型如所示。
. bayesian network model
. 贝叶斯网络模型
在该模型中结果节点“resultnode”的直接影响要素包括“worst area”、“worst radius”、“perimeter error”,“worst area”的影响路径包括直接影响路径“worst area”→“resultnode”和间接影响路径“worst area”→“worst radius”→“resultnode”,“worst radius”的影响路径只有直接影响路径“worst radius”→“resultnode”,“perimeter error”的影响路径包括直接影响路径“perimeter error”→“resultnode”和4条间接影响路径,分别是“perimeter error”→“radius error”→“area error”→“worst area”→“worst radius”→“resultnode”,“perimeter error”→“radius error”→“area error”→“worst area”→“resultnode”,“perimeter error”→“area error”→“worst area”→“worst radius”→“resultnode”,“perimeter error”→“area error”→“worst area”→“resultnode”。
取第二个样本作为待测试样本。该样本结果节点取值为0,表示乳腺癌良性,计算结果表示“worst area”节点存在交互效应节点“worst radius”,说明“worst area”在对“resultnode”产生直接影响的同时,通过影响“worst radius”对“resultnode”产生间接影响,考虑因素之间的交互效应,首先预测当前样本结果节点取值为0的概率,然后改变样本中“worst area”节点的值,同时将交互效应节点“worst radius”的值不设定,预测结果节点取值为0的概率。将这两个概率做差,得到“worst area”对结果节点的影响度为0.9935。“worst radius”节点不存在交互效应节点,只对“resultnode”产生直接影响,首先预测当前样本结果节点取值为0的概率,然后改变“worst radius”节点取值,预测结果节点取值为0的概率。两个概率做差,计算“worst radius”节点对结果节点的影响度为0.9935。“perimeter error”节点存在交互效应节点“radius error”、“area error”,与“worst area”影响度的计算类似,计算结果为“perimeter error”节点影响度0.0347。可见“worst area”和“worst radius”是影响第二个样本“resultnode”判定为良性的主效应因素。
取第20个样本作为待测样本。该样本结果节点取值为1,表示结果为乳腺癌恶性。计算结果表示“worst area”、“worst radius”、“perimeter error”节点都不存在交互效应节点,只对“resultnode”产生直接影响,只需计算当前考虑节点取值变化前后对预测概率的影响即可,计算结果中“worst area”、“worst radius”、“perimeter error”节点影响度分别为0.035、0、0.001,因此判定“worst area”为影响第20个样本结果判定为恶性的主效应因素。
4.4. 对比分析
实验结果中,对于第二个样本,如果不考虑因素之间的交互效应,“worst area”对结果节点的影响度只有0.2085,得到的结论是:“worst radius”是影响第二个样本“resultnode”判定为良性的主效应因素。这与考虑交互效应得到的分析结论是不一致的。这是因为“worst area”取值变化直接影响了“worst radius”的取值,如果忽略了“worst area”和“worst radius”之间的关联关系,就可能导致片面的结论。
5. 结论
本文提出的主效应因素分析方法在利用贝叶斯网络模型进行主效应因素分析的过程中,利用网络结构模型筛选存在交互效应的因素,同时考虑因素之间的交互效应以及这些因素共同对结果产生的影响,从而得到主效应分析结论。实验证明,与现有方法相比,本文方法克服了单因素分析方法将因素孤立化的问题,在充分分析因素之间的联动交互影响的基础上提取主效应因素,提高了主效应因素分析结论的合理可信性。
致谢
对本文的创作给予指导和帮助的同事朋友,在此一并感谢。
基金项目
本文受到装备预研项目“云化服务xx验证技术”(no: 315105307)、国防科技项目“xx跨域体系集成与试验验证技术”(no: 2019-jcjq-zd-193-00)等资助。