1. 引言
太阳系的角动量对于太阳系的形成和演化来说是一个非常重要的物理量,要计算太阳系的角动量首先要算出太阳的自转角动量。太阳的自转并不是均匀自转,而是存在较差自转 [1] [2] 。schou等人描绘了太阳包层区域自转的二维景象:在赤道附近、0.9 r☉深处的自转角速度是最快的,约为460 nhz;在两极附近的自转角速度是最慢的,约为310 nhz;在0.7~1.0 r☉的深度范围内,太阳的自转角速度随纬度变化比较明显;而在0.5~0.7 r☉的深度范围内,太阳的自转角速度几乎不随纬度变化,都是430~440 nhz [3] 。在计算太阳的自转角动量时,一般都是根据太阳自转角速度随深度和纬度的分布来求出太阳的平均自转角速度,然后乘上太阳的转动惯量,求出太阳的自转角动量。
以前由于受观测条件和传统观念的限制,人们认为太阳系的边界就是海王星(或者冥王星),太阳系的角动量就是太阳的自转角动量加上已经观测到的大行星的轨道角动量;于是得出了太阳的自转角动量约占太阳系总角动量1%的结论 [4] 。可是最近20多年的观测表明,海王星轨道之外还有很多小天体,大部分是千米大小的星子,聚集成的脏雪球;这块区域称为柯伊伯带,是短周期彗星(周期短于200年)的主要来源 [5] 。周期大于200年的彗星称为长周期彗星,人们认为它们来自太阳系最遥远的部分。荷兰天文学家扬·奥尔特(jan·oort)通过研究长周期彗星的轨道和数目,提出存在一个巨大的、大致呈球形的彗星仓库(奥尔特云)环绕着我们的行星系,从柯伊伯带外侧一直延伸到大约105 au [5] - [9] 。奥尔特云由于距离遥远,并没有被直接观测到,可是人们观测到了起源于奥尔特云的彗星,奥尔特云的范围就是根据这些彗星推测出来的 [10] 。
恒星和行星的形成理论表明:在恒星的形成过程中,较小的次星可能会被其主星抛射到外围 [5] 。理论计算表明在距离太阳至少几千au的轨道上可能存在一颗类木行星 [11] 。这个天体的质量很大,也可以称为太阳伴星。太阳伴星可能一开始位于柯伊伯带,然后不断地把它周围的彗星向内抛射,而它自身的轨道逐渐向外迁移,一直外移到现在的位置 [12] 。太阳伴星也有可能原来是一颗“流浪行星”,后来才被太阳系捕获 [9] 。天文观测虽然没有直接探测到太阳伴星,但是也不排除其存在的可能性 [11] 。
凡是太阳引力起支配作用的区域都可以称为太阳系的范畴,太阳的比邻星——南门二丙星(半人马座α星)距离太阳约为4.3光年,太阳近邻恒星之间的平均距离约为3光年 [5] ,所以太阳系的半径大约为1.5光年。行星在围绕太阳公转时,轨道半径越大,轨道角动量就越大。在计算太阳系的角动量时,如果仍然仅仅考虑太阳的自转角动量和八大行星的轨道角动量就显得太狭隘和保守了。本文将会根据最近的理论研究和观测数据,考虑柯伊伯带、奥尔特云和太阳伴星等天体的轨道角动量来计算整个太阳系的角动量,算出的结果可能会与传统意义上的太阳系的角动量大不相同。
2. 角动量的计算方法
2.1. 太阳的自转角动量
我们用1995版的eggleton’s恒星演化程序来计算太阳演化,获取演化数据 [13] - [18] 。对流超射系数采用0.12 [19] [20] ,初始金属丰度采用0.02 [18] ,金属元素混合模式采用的是grevesse与sauval (1998)标准太阳模式 [21] 。我们用opal高温不透明度表 [22] [23] 和wichita大学低温不透明度表 [24] 编译了与eggleton’s恒星演化程序相匹配的不透明度表 [25] [26] 。
eggleton’s恒星演化程序将恒星分成199层,每个壳层内密度、温度、化学丰度等参量都相同。但是,不同壳层的厚度并不相同,通常核心区的壳层分的薄一些,包层区的壳层分的厚一些。太阳的密度从中心到表面变化太大,用均匀球模型计算转动惯量会产生很大的误差。所以首先要精确地计算每一个壳层的转动惯量,然后再求和,算出太阳总的转动惯量。第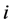 个壳层的外半径是
个壳层的外半径是 ,半径为
,半径为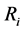 的球壳内的总质量是
的球壳内的总质量是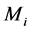 ;第
;第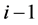 个壳层的外半径是
个壳层的外半径是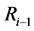 ,半径为
,半径为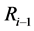 的球壳内的总质量是
的球壳内的总质量是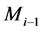 。则第
。则第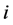 个壳层的质量为
个壳层的质量为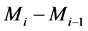 ,第
,第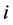 个壳层的外半径和内半径分别为
个壳层的外半径和内半径分别为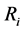 和
和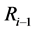 ;第
;第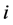 个壳层的密度为
个壳层的密度为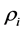 ,
,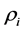 必然满足:
必然满足:
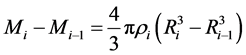 。 (1)
。 (1)
根据转动惯量的定义,可以求出第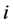 个壳层的转动惯量:
个壳层的转动惯量:
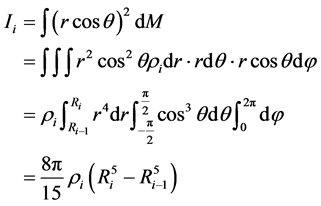 。 (2)
。 (2)
联立(1)、(2)式,可得
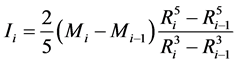 。 (3)
。 (3)
最里面的一个壳层其实是一个实心的球体,因此,太阳总的转动惯量为:
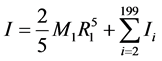 。 (4)
。 (4)
如果太阳的平均自转角速度为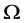 ,则太阳的自转角动量为:
,则太阳的自转角动量为:
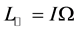 。 (5)
。 (5)
2.2. 行星在正圆轨道上公转的角动量
行星围绕太阳公转,万有引力提供向心力:
 。 (6)
。 (6)
行星公转的轨道角动量:
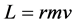 。 (7)
。 (7)
联立(6)、(7)二式,可得:
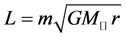 。 (8)
。 (8)
2.3. 行星在椭圆轨道上公转的角动量
行星轨道半长轴为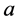 ,椭率为
,椭率为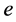 ;则近日点距离
;则近日点距离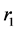 和远日点距离
和远日点距离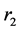 分别为:
分别为:
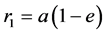 ,
,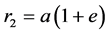 。 (9)
。 (9)
行星绕太阳公转,受到太阳的引力为有心力,行星的轨道角动量守恒;而且在近日点和远日点,行星的公转速度方向与矢径方向垂直,必有:
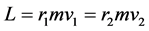 。 (10)
。 (10)
行星受到太阳的引力也是保守力,机械能守恒:
 。 (11)
。 (11)
联立(10)、(11)二式,可得:
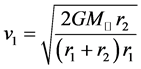 ,
,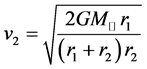 。 (12)
。 (12)
联立(9)、(10)、(12)三式,可得:
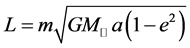 。 (13)
。 (13)
3. 太阳系的角动量
3.1. 太阳的自转角动量
太阳现在的演化寿命为45.7亿年 [27] 。eggleton’s恒星演化程序的计算结果表明,当太阳的演化寿命为45.7亿年时,半径也恰好是1.00 r☉。根据eggleton’s恒星演化程序的相关数据,采用公式(3)和(4),可以算出太阳现在的转动惯量为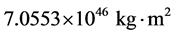 。而观测表明太阳现在的平均自转角速度是
。而观测表明太阳现在的平均自转角速度是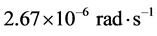 [28] ,根据公式(5)可以求出太阳现在的自转角动量为
[28] ,根据公式(5)可以求出太阳现在的自转角动量为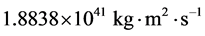 。
。
3.2. 八大行星的轨道角动量
水星、金星、地球、火星、木星、土星、天王星和海王星是太阳系中早已确认的八大行星;八大行星的轨道半长轴,我们引用的是allen (1973)的数据 [29] ;八大行星的轨道椭率和质量,我们引用的是杨大卫(2003)的数据 [30] ;根据公式(13)可以分别求出八大行星围绕太阳公转的轨道角动量,详见表1。由于这几颗大行星的公转平面都很接近黄道面,所以八大行星总的轨道角动量可以近似认为是这八个行星的轨道角动量的代数和,即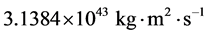 。
。
3.3. 小行星带的轨道角动量
小行星带主要位于火星和木星轨道之间,虽然数量众多,可是它们的总质量却仅为(或者小于)地球质量的千分之一。小行星的轨道半径都采用小行星主带的平均半径2.65 au [31] ,小行星距离太阳比较近,轨道椭率一般都不大,我们近似认为小行星都在正圆轨道上绕日公转。根据公式(8),可以算出小行星带的轨道角动量为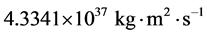 。
。
. the orbital momentum of the eight giant planets in the solar system
表1. 太阳系八大行星的轨道角动量
3.4. 柯伊伯带的轨道角动量
柯伊伯带是位于海王星轨道外侧的一个散布大量小天体和矮行星的环状区域,它们是原始太阳星云的残留物,也是短周期彗星的来源。如今已有1000个左右的柯伊伯带天体被发现,直径从数千米至上千千米不等。柯伊伯带距离太阳约30~50个天文单位,其总质量约为(或者小于)地球质量的十分之一 [5] 。
柯伊伯带天体的轨道椭率小于或者等于0.8 [32] ,我们采用中间值0.4;轨道半长轴统一采用40 au [33] 。根据公式(13),可以算出柯伊伯带天体的轨道角动量为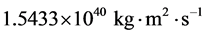 。
。
3.5. 奥尔特云的轨道角动量
在柯伊伯带外面的更远处,有一个大致呈球形分布的彗星仓库——奥尔特云。奥尔特云向外可以一直延伸到大约105 au。彗星的密度一般介于200至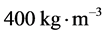 之间 [34] ,我们采用中间值
之间 [34] ,我们采用中间值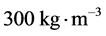 。奥尔特云中半径大于1千米的彗星不少于1013颗 [5] 。我们近似认为奥尔特云包含1013颗半径为2千米的彗星和1013亿颗半径为0.5千米的彗星,就可以估算出奥尔特云的总质量:
。奥尔特云中半径大于1千米的彗星不少于1013颗 [5] 。我们近似认为奥尔特云包含1013颗半径为2千米的彗星和1013亿颗半径为0.5千米的彗星,就可以估算出奥尔特云的总质量:
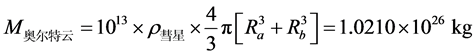 。 (14)
。 (14)
柯伊伯带天体的轨道椭率小于或者等于0.8;奥尔特云更加遥远,轨道更扁,平均椭率可以直接采用0.8,平均轨道半长轴采用50,000 au。根据公式(13),可以算出奥尔特云中所有彗星的轨道角动量的代数和为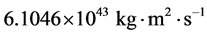 。奥尔特云呈球形,所以奥尔特云总的角动量不能采用代数求和,而应该采取矢量求和。奥尔特云在黄道面上的运动对角动量有贡献,而与黄道面垂直的运动所产生的角动量会互相抵消。所以,奥尔特云角动量的矢量和为:
。奥尔特云呈球形,所以奥尔特云总的角动量不能采用代数求和,而应该采取矢量求和。奥尔特云在黄道面上的运动对角动量有贡献,而与黄道面垂直的运动所产生的角动量会互相抵消。所以,奥尔特云角动量的矢量和为:
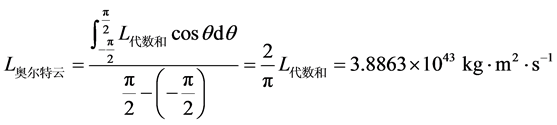 。 (15)
。 (15)
3.6. 第九大行星的轨道角动量
batygin与brown通过观测柯伊伯带天体的轨道,发现了轨道异常。他们通过数学模型和电脑模拟表明,如果这些轨道异常是随机现象,出现的概率仅为0.007%。所以,他们认定是由于动力源而引起了柯伊伯带天体的轨道异常,这个动力源就是柯伊伯带之外的一颗大行星,称之为太阳系的第九大行星。他们的电脑模拟给出了一个可能的结果:第九大行星的轨道半长轴为700 au,轨道椭率为0.6,质量约为(或者大于) 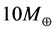 [35] 。根据公式(13),可以算出第九大行星的轨道角动量为
[35] 。根据公式(13),可以算出第九大行星的轨道角动量为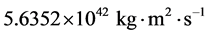 。
。
3.7. 太阳伴星的轨道角动量
关于太阳伴星的轨道参数,matese与whitmire给出了比较精确的数值:太阳伴星的质量大于(或者约等于) 7倍木星质量,轨道半长轴小于(或者约等于) 6000 au,椭率的平方小于(或者约等于) 0.5 [36] 。根据公式(13),可以算出太阳伴星的轨道角动量为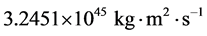 。
。
3.8. 太阳系总的角动量
对太阳的自转角动量以及八大行星、小行星带、柯伊伯带、奥尔特云、第九大行星和太阳伴星的轨道角动量求和,就可以算出太阳系总的角动量:
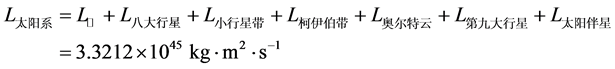 (16)
(16)
由于受理论研究和天文观测的限制,传统上的太阳系的角动量主要包含太阳的自转角动量与八大行星的轨道角动量;我们的计算结果表明这两部分之和为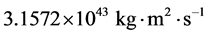 ,太阳的自转角动量只占0.60%。严格来讲,太阳系的角动量还应该包括行星的自转角动量、卫星的自转角动量和卫星绕行星公转的轨道角动量;可是这些角动量比八大行星的轨道角动量小很多,所以我们在计算过程中,没有考虑这些角动量。
,太阳的自转角动量只占0.60%。严格来讲,太阳系的角动量还应该包括行星的自转角动量、卫星的自转角动量和卫星绕行星公转的轨道角动量;可是这些角动量比八大行星的轨道角动量小很多,所以我们在计算过程中,没有考虑这些角动量。
根据我们的计算结果,可以对太阳系内各种天体的角动量进行重新排序。第一是太阳伴星的轨道角动量,如果太阳伴星真的存在,整个太阳系97.71%的角动量将会集中在太阳伴星上。第二是奥尔特云的轨道角动量,奥尔特云的总质量虽然不大(相对于木星),可是由于它们距离遥远,轨道角动量却很大,占整个太阳系角动量的1.17%。第三是八大行星的轨道角动量之和,占整个太阳系角动量的0.95%。第四是第九大行星的轨道角动量,占整个太阳系角动量的0.17%。第五是太阳的自转角动量,仅占太阳系总角动量的0.0057%。第六是柯伊伯带的轨道角动量,仅占太阳系总角动量的二十万分之一。第七是小行星带的轨道角动量,仅占太阳系总角动量的亿分之一。
4. 讨论
戴文赛先生给出的太阳系的角动量是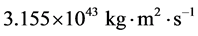 [37] ,这其实就是传统上的太阳系的角动量;而我们算出的相应结果是
[37] ,这其实就是传统上的太阳系的角动量;而我们算出的相应结果是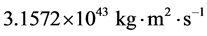 ,二者的相对误差仅仅有0.07%。johnstone等人算出的太阳转动惯量为
,二者的相对误差仅仅有0.07%。johnstone等人算出的太阳转动惯量为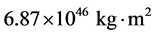 [28] ,而我们算出的太阳转动惯量为
[28] ,而我们算出的太阳转动惯量为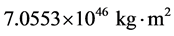 ,二者的相对误差仅为2.7%。pijpers给出的太阳自转角动量为
,二者的相对误差仅为2.7%。pijpers给出的太阳自转角动量为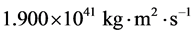 [38] ,而我们算出的太阳自转角动量为
[38] ,而我们算出的太阳自转角动量为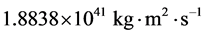 ,二者的相对误差仅为0.85%。
,二者的相对误差仅为0.85%。
如果太阳伴星存在,那么太阳系几乎全部的角动量都会集中在太阳伴星上,可是要想直接观测到太阳伴星却很困难。一方面太阳伴星距离太遥远,其反射的太阳光极其微弱;另一方面,太阳系已经形成几十亿年,太阳伴星早已经冷却,其红外辐射也非常微弱。探测太阳伴星就已经非常困难,在相同条件下探测太阳系外寄主恒星的遥远伴星就更加困难了。可是最近deacon等人仔细研究了tyc9486-927-1恒星和2mass j21265040−8140293行星后发现二者存在协调运动,后者并不是“流浪行星”,而是前者的遥远伴星 [39] 。2mass j21265040−8140293行星之所以能被观测到,得益于它自身很年轻,该行星在收缩过程中,释放了很多引力势能,使自身升温,现在向外辐射出较强的红外线,有幸被观测到。
通过观测数据可以推算出2mass j21265040−8140293行星的质量为11.5至15倍木星质量,距离其寄主恒星tyc9486-927-1为4450至5700 au [39] 。而matese与whitmire计算出太阳伴星的质量大于(或者约等于) 7倍木星质量,太阳伴星的轨道半长轴小于(或者约等于) 6000 au [36] 。太阳伴星在质量和轨道半径两方面都与2mass j21265040−8140293行星非常接近。所以,我们应该重新评估tyc9486-927-1恒星和2mass j21265040−8140293行星系统的观测价值,它们不仅仅是目前观测到的距离最遥远的恒星–行星系统,它们很像太阳–太阳伴星的早期景象,它们可以被看作太阳伴星存在的间接观测证据。
我们算出的太阳系的总角动量是传统上的太阳系的角动量的105倍,这对太阳系的形成来说,影响很大。太阳系是由星云塌缩而成,在塌缩的过程中,可以近似看成孤立系,角动量守恒;算出太阳系现在的总角动量的修正值,就等于算出太阳系原始星云的自转角动量的修正值。太阳在形成的过程中需要不断向外转移角动量;传统上认为太阳本身只保留大约1%的角动量,其余的角动量都转移给了行星系统;而我们算出的太阳系总角动量的修正值表明太阳本身只保留大约万分之一的角动量,需要向外转移更多的角动量。太阳也是一颗普通的恒星,太阳系总角动量的修正值对于研究系外恒星–行星系统的角动量很有参考价值,对于恒星形成的理论研究也有参考价值。
基金项目
本项研究工作得到了普洱学院自然科学基金(基金号:k2015030)、云南省教育厅自然科学基金(基金号:2012y和2014y)和国家自然科学基金(基金号:11265012)的支持。