1. 引言
近年来,伴随着城市交通需求的持续增长,公共交通发展面临严峻的挑战。公共客运交通系统基础薄 弱,服务水平较低,轨道交通的开发和城市道路大面积扩张重修使城市的道路结构迅速发生变化,公交系统的载客效率越来越低,高峰期交通拥堵日益严重。如何对公交网络的行车线路进行优化,对接驳进行改善等等来缓解交通压力,提高出行效率是关系到城市发展的重要问题。而对公交系统的优化问题,正是在处于这种背景下越来越多地得到人们的关注。
2. 公交网络设计问题的概述
公交系统的优化问题首先要从多个维度对现有公交网络进行评估,继而找出评估中不符合期望的因子。运用多种算法,建立模型,对期望值较低的因子进行优化。并以软件为基础,运行实际优化模型并进行改善。最后将改善后的优化模型投入实际应用,通过对路线的进一步规划等等来达到优化的目的。本文主要从算法,软件和应用三个方面,通过研究汇总各界对该问题的研究与成果,介绍了一系列算法及其基于软件的可视化操作,并列出了实际背景下的一系列运用,以期对公交网络的优化问题进行全方位的综述。
3. 公交网络设计问题
公交网络设计问题(transit network design problem, tndp)一般指:在一定的交通资源限制条件下,以公交系统的某项指标为优化目标,求取交通线网布局及调度的最佳选择的问题。tndp存在着影响因素多,数据复杂度高,数据需求量大等特点,且通常此问题具有非线性非凸性的特点,又具有多目标性,求解其最优解具有相当的困难。一般认为tndp属于nph (non-deterministic polynomial-hard)问题,不能用精确算法求解。
3.1. 研究方法
对于一个给定的城市公交系统,它的合理性可以由两类指标刻画,可以是静态的指标,如公交线网密度,站点覆盖情况,重复系数,非直线系数等,也可以是动态的指标,如全线客流,合计路段流量,换乘系数,平均乘距等 [1] 。显然静态的指标并不是能随意变化的,这类指标具有相对的稳定性,对这类指标的优化通常需要较大的成本来改造公交线网。而动态的指标则具有随机性,通常可以通过对公交频率的调整来对这些指标进行优化。
以上两类指标,可以总结为对线路网络的优化和对发车频率的优化,在优化城市公交系统时,既可以先单纯考虑线路网络的优化设计,再在规划好的线网上对发车频率优化,也可以联合考虑两方面优化。例如,lampkin 和 saalmans [2] 中给出了单独考虑公交线网设计,再考虑发车频率的思路;ceder和wilson [3] 的基本思想也是如此,提出三阶段法:1) 出行分配;2) 路径规划;3) 确定发车间隔。也有将两方面联合考虑进行优化的例子,如bajj和mahmassani [4] 提出了rga(route generation algorithm),选取最大od需求点,同时优化线路和频率,再在得出的线网进行分析,以决定是否选择此线网。mauttone和urquhart [5] 对此做出改进,将最大od需求点改为合适的od需求点,亦是联合优化线网络与频率的例子。lee [6] 在常规公交网络优化中综合优化线路走向与发车时间间隔,并考虑了线路乘车与等车时间的相互关系,之后又考虑了了交通方式划分,并通过启发式算法求解。
通常情况下,将两类指标分开考虑的模型的思路更为简单,当然也有例外。例如,王炜 [7] 提出的“逐条布设、优化成网”法也属于综合考虑进行优化,此方法将诸多的约束条件在线网布设过程中或在最后的流量检验、线网调整过程中进行考虑,使得此方法较为简洁。
3.2. 求解算法
tndp的模型通常涉及到组合最优化问题,这是tndp问题本身的内在原因决定的,而这些模型的最优解又是不容易得到的,有些模型目前无法求得最优解,因此,我们考虑用启发式算法来解决tndp的模型求解问题。
启发式算法是相对于最优化算法提出的,它可以给出约束条件下的可行解,但其与最优解的差距并不能得到保证。
遗传算法是基于darwin的进化论和mendel的遗传学说提出的启发式算法。在此算法中,研究对象被称为染色体,它的特征被记录成编码,称为基因。在算法中有三个基本操作:1) 选取适应度高的个体,淘汰适应度低的个体,称为“选择”;2) 迭代中父代个体部分基因交替重组,称为“交叉”;3) 改动个体的某些基因值,称为“变异”。遗传算法的伪代码如下:
g:终止进化次数
m:种群规模
p- old:父代种群
p-new:子代种群
f(x):计算个体x的适应度
fmax:满意的适应度
pc:交叉发生的概率
pm:变异发生的概率
for n = 1: g
for i = 1: m
ifmin(f(p-new(j))) < f(p-old(i))
以p-old(i)替代p-new中适应度最低的p-new(j)
end
if max(f(p-new(j))) > fmax
终止算法输出p-new
end
end
while没有生成够m个新个体
按适应度算法选取p-old中的两个元素p-old(i)与p-old(j)
ifrand(0,1) > pc
由p-old(i)与p-old(j)经交叉操作生成两个新个体,存入p-new中
end
ifrand(0,1) > pm
由p-old(i)与p-old(j)经变异操作生成两个新个体,存入p-new中
end
end
end
g fusco等人 [8] 提出了采用遗传算法选择次优的路线的方法,在理论上解释了遗传算法在tndp中的可行性。韩印 [9] 从公交线网发车间隔这一角度出发,构造了公交调度优化模型,将遗传算法引入到模型求解中,证明了遗传算法在这一问题求解上的实用性和可靠性。
蚁群算法是dorigo等人 [10] 受蚂蚁搜索食物的启发,提出的一种启发式算法,起初用来解决tsp问题(traveling salesman problem)等组合优化问题。昆虫学家的研究表明,蚂蚁在寻找食物时能够在其走过的路径上分泌一种信息素,这种信息素可以被其它蚂蚁感知,蚂蚁倾向于向信息素浓度高的地方移动,而信息素的浓度则会随着时间减小。蚂蚁的这种特性,使得信息素浓度实现了正反馈调节,即信息素浓度更高的地方增长的可能性更大,最终使得蚂蚁集体在搜索食物时总是能够沿短路搜索 [10] 。蚁群算法的基本流程如下:
1) 初始化:取蚂蚁m只,路径n条,将蚂蚁随机分配到路径上
2) 对蚁群整体做出评价,满足条件则输出路径,否则继续
3) 按蚂蚁经历的路径释放信息素
4) 根据信息素浓度按概率选择合适的路径
5) 降低全局信息素浓度,回到2)
于景飞 [11] 分析了蚁群算法在tndp中的可行性,详细研究了如何利用蚁群算法来对城市公交线网进行优化。于滨 [12] 采用粗粒度模型的并行蚁群算法,求解了一个以直达客流密度最大为目标的公交线网优化模型,得到了很好的效果,在保证解的质量的同时具有较快的收敛速度。
模拟退火算法最早是由metropolis等人 [13] 提出的,思想来源于固体退火原理,是一种利用随机取值避免局部最优解的方法。kirkpatrick等人 [14] 于1983年将它的思想应用于组合优化领域。fan和machemehl [15] 建立了tndp的多目标非线性整数模型,首次采用模拟退火算法对tndp进行求解,并证明模拟退火算法一定程度上优于遗传算法。郑小花等 [16] 建立了以乘客等车时间最小为优化目标的公交优化调度模型,也模拟退火算法对模型进行求解,并以实际的运营数据对结果进行检验,进一步证明此方法是有效可行的。
禁忌搜索算法最初由glover于1986年提出并做了大量研究 [17] ,白子建 [18] 提出了一类以运营效益为目标的公交调度模型,使用禁忌搜索算法优化,通过仿真试验证明此算法优化是有效的。
还有些研究综合使用了多种算法,例如周媛 [19] 提出了以交通效率最大化为总目标的优化模型,求解释先使用遗传算法进行全局搜索,再用禁忌搜索算法进行局部搜索。此算法有效结合了两个算法的特点,在收敛性能和避免局部最优方面都有较大改善。又如,任传祥 [20] 使用遗传算法和模拟退火算法的混合算法,对标准的遗传算法进行改进,提高了算法的效率。赵志军 [21] 则融合了蚁群算法和遗传算法求解了一个公交网络的多目标优化模型。
3.3. 模型构建
在研究方法中,我们提到了单独考虑公交线网设计,再考虑发车频率的方法,其实质是运用了双层规划的思想,双层规划模型是目前公交网络设计中使用较多的模型。leblanc [22] 最早明确地将双层规划模型引入到网络设计问题中,对此模型的研究开始兴起。所谓双层规划模型是一种具有双层递阶结构的系统优化模型,一般形式如下 [23] :
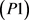
其中
如下决定:
其中,
分别是上层(p1)与下层(p2)的决策变量,
与
是上、下层的目标函数,求解双层规划模型时,先求得(p2)的最优解
,再带入到(p1)求得最优解
,便得到双层规划的最优解
。
单连龙和高自友 [24] 根据公交网络的具体特点,提出了一个上层模型为标准公交网络设计模型,下层模型是一个公交网络平衡配流模型的双层规划模型,并通过灵敏度分析解释了此模型可以得到有效解。
于滨等人 [25] 则建立了一个以频率优化模型为上层模型,以公交客流分配模型为下层模型的双层规划模型,经过数据测试验证也是一个有效的模型。
tndp的模型建立通常依实际问题采取不同的策略,在分步求解问题时也可能会构建多个模型,除了双层规划模型还有许多有效实用的模型。
胡启洲、张卫华 [26] 用定量分析法把公交线网中的主要优化目标及约束条件用函数关系表示,在定义最佳方案点的基础上,以目标函数为因素指标集,以备选方案为论域集,利用灰色系统的关联度知识,建立了城市公交线网优化的定量决策模型。
张东旭 [27] 以k-means聚类算法为基础,在此基础上融合iso-data算法进行聚类分析,通过k-means 算法快速计算出聚类中心,结合已有公交线路生成合理的定制公交线路模型。
付波飞 [28] 提出公交停靠站点的通行能力与道路交通条件、站点上游信号灯配时、乘客上下车时间、公交车进出站时间等等有很大关系,提出站点通行能力计算方法,从而得出一个停车泊位数单位时间内所能停靠的最大车辆数,进而对公交站点进行合理规划。
4. 轨道交通影响下的公交网络设计
4.1. 问题描述
公交和地铁是城市公共交通系统中最核心的两个组成部分。近年来,我国许多城市虽大力推广轨道交通的使用,但地面交通的分担率却没有显著提升,其中原因值得深究。为解决大城市客运交通拥挤、事故频发、投入与成效不成正比的问题,缓解城市交通需求与实际供应之间的矛盾,必须给出行之有效的优化方案。
公共交通方式主要有:公交、地铁和轻轨三种。公交的投资较小,经停地点多,但是舒适度和受地面交通影响较大,适合市民的中短途出行。地铁具有速度快、里程远、载客量大的优点,准点率高且辆次多,适合中长距离的出行。轻轨的各项指标介于以上二者之间。本文所指的轨道交通主要是地铁和轻轨。
很多市民发现,地铁站下车后,要转乘公交很不方便——不能直接公交车站,如果要到就近的换乘枢纽乘公交,需走天桥绕行近半小时。对此,目前多地已增开公交,接驳地铁各出站口至公交枢纽站。轨道交通车站与常规公交车站的衔接设施非常有必要,这影响地铁吸引范围内出行者出行方式额选择,促使客流在各种交通方式之间进行重新分配。
轨道交通的出现,使得常规公交出行客流发生了一下几种变化 [29] :
1) 起止点均在轨道交通一次吸引范围内,轨道交通覆盖出行全过程,常规公交客流量转移至轨道交通,且注意比例随着出行距离而增加;
2) 起止点一端在轨道交通一次吸引范围内,轨道交通与常规公交配合完成出行,与轨道交通接驳的公交站客流量增加,单纯使用公交出行的客流量随着出行距离的减少而减少;
3) 起止点均不在轨道交通一次吸引范围内,时间和票价的阻扰作用较大,常规公交客流量转移到轨道交通的可能性小。
为探究轨道交通开通后公交系统的优化问题,相关研究及论文应运而出。
4.2. 模型与算法
李铁军 [30] 分析了车站客流的时空分布特征并基于车站周边用地和基于车站区位提出了两种具体的分类方法,再通过对比两种分类方法的分类结果,研究了各类别中不同换乘方式所占比重,得到了不同车站类别对应的主要换乘方式。
罗艺、钱大琳 [31] 运用space l和space p方法分别构建了北京市公交—地铁复合网络及其子网络.实证研究了公交—地铁网络的基本拓扑性质并对复合网络及其子网络的网络特性进行比较,从整体的角度,综合性地分析城市公共交通运输网络的特性及换乘状况。
徐勇等人 [32] 构造公交地铁网络的标号模型及映射网络模型,以适当倍数缩小地铁线路上站点之间的权值,进而可将公交与地铁进行一体化处理,缩小后可使地铁线路具有明显的优势以达到优选地铁的目的。运用映射网络图、二分图、半张量积等理论给出了公交地铁一体化网络的最优路选择算法。
魏超、龙建成 [33] 构建了城市轨道交通双边接驳公交线路优化模型,对接驳公交线路布局以及开行频率进行优化。根据模型特点,设计了人工蜂群算法。为了提高算法的计算效率和稳定性,采用了多种邻域搜索策略,且对算法的相关参数进行了校正。
孙杨等 [34] 提出基于轨道交通新线的常规公交网络优化调整方法。从定量化的角度提出常规公交候选线路的生成算法,提出常规公交网络优化调整的多目标模型,同时优化调整常规公交线路走向与运营参数,设计求解模型pareto解集的启发式算法,该方法无需预先给出多个优化目标的权重,避免传统公交网络优化中人为确定优化目标权重的主观性。
徐勇等 [35] 通过建立公交地铁网络图及基于此网络图的二分图,映射网络图,并对地铁线路上站点间的权值进行合理倍数的缩小以达到优选的目的。
徐志强等 [36] 将遗传算法与粒子群算法进行了比较,结合轨道交通接运公交线网优化区域离散化思想,以粒子群算法为基础计算求解最优接运公交线网。
5. 公交网络设计实例
5.1. 都江堰城市公交网络设计方法应用
都江堰市位于成都平原西北,城市道路网结构形式是环线、放射线加棋盘线。其公交系统以公共汽车为主。全市拥有标准公交车辆108台,运营车辆数91台。经调查线路公交汽车高峰小时满载率为75.896,大公共汽车平均营运速度14.36 km/h,小公共汽车平均营运速度为14.l km/h。
从考虑乘客与公交企业两者的利益出发,将所建立的模型综合运用于都江堰市公交系统,运用遗传算法对公交线网进行优化,将线网分为干线网优化和普线网优化,并结合既有公交线网调整的方法,选取合理的规划参数,以期使都江堰市公交线网得以优化。优化之后,通过对都江堰公交线网优化总体指标的评价可以发现:同现状年线网相比,2010年公交线网的总长度为现状年的2.6倍,路网密度增加了106。优化线网的线路重复系数较现状明显降低,说明线网空间分布合理。公交线网密度是反映居民接近线路程度的重要指标,线网密度由现状的0.33 km/km2,提高到2010年的0.68 km/km2。其中人口最密集的中心区和外围区线网密度有了很大的提高,对于改善都江堰市公交拥挤状况有着积极作用,在市郊区受道路网和地形条件限制,线路网密度提高幅度不大。但市郊区域内公交线路充分利用了区内次干道以上的道路以及能通公交车的道路,因此外围区的公交路网密度是适宜的。
5.2. 西安市公交线网设计研究及其运用
20世纪90年代以来,西安市的公共交通事业有了长足的发展,公交营运线路由1990年的54条增加到2007年的234条,营运线路总长度由1994年的804.8 km增加到2007年的3312 km,线路网长度由1996年的441.4 km增加到1999年的3726 km。
公交线路网密度、线路密度及线路重复系数是反映城市居民接近公交线网程度的重要指标。在分析这三个指标时,按照行政区划、城市土地利用性质、交通区位线等因素把西安市区划分为33个小区,通过数据比较发现:西安市中心市区及大部分小区公交线网密度偏低。故采用如下的优化步骤对西安市公交线网的进行优化:1) 输入调查获得的西安市公交乘客od矩阵,根据优化目标建立的公交线网优化目标函数。2) 布设第一条主干线线路,在每个一级公交起(讫)点上放置一个人工蚂蚁,根据客流量和节点间距确定蚂蚁从该公交站点到其相邻公交站点的转移概率,并取转移概率最大者运动到下一个公交站点(网络节点)。3) 布设第二条主干线路,修改直达乘客量矩阵,从原直达乘客量矩阵中减去第一条线路运送得直达乘客量。4.得出各个蚂蚁经过的路径长度,判断是否满足约束条件,得出直达率及总的费用值。5.输出满足目标函数的公交线路,并对线网进行调整。
按上述评价指标,统计优化线网的各项评价指标,得公交线网密度2.78 km/km2,线网覆盖率达到97.3%,根据《城市道路交通规划设计规范》,理论上城市中心区公交线网密度一般为3~4 km/km2,城市边缘地区一般为2~2.5 km/km2,与西安市公交线网现在线网密度为2.2 km/km2,线网密度有所提高,同时也达到了基本覆盖率,综合分析比较各项评价指标结果可知,本次公交线网优化的结果是比较令人满意的。
5.3. 保定市公交网络设计的具体运用
保定市隶属于河北省,下辖4区5市18县,全市总面积22,206 km2,其中城区面积为312 km2,城区人口在2013年达到108.9万人,根据新标准,保定市已经达到大城市的规模。保定市城市道路呈方格状布局,主干道为“五横五纵二环”,目前保定市城市快速路有68.2公里、主干道196.5公里、次干道146.8公里,支路287.3公里,道路网络的特点为快速路较多而此干路偏少。依据线路在网络中的换乘作用以及线路的非直线系数,旨在减少乘客乘车距离、换乘次数和线路非直线系数(换乘比例反映了线路在网络中的换乘作用,其值越大表明线路在网络中的换乘作用越小)。先通过建立标准化评估因子,对保定市公交线路的每条网络进行评估,根据评估结果,删除一定数量评估因子过大的线路,根据删除后整个网络的od的需求情况,使用贪婪算法生成与删除数量相同的初始线路,最后利用蜂群算法对生成的线路进行改进,获得最优线路。
优化结果表明:通过线路的调整,去除了6条对网络换乘次数影响较小的线路,增加了6条新的线路,不但使得网络的平均换乘次数与平均乘车距离相应减少,而且线路平均非直线系数有了相应的减少,整个网络的服务水平有了明显的提高。实例说明所设计网络优化方案能较好改善网络的结构,有效提高网络服务效率。
6. 基于transcad的公交网络设计研究
transcad是由美国caliper公司开发的强有力的交通规划和需求预测软件。trans cad的出现与发展使得求解大规模模型变得不再困难,继而衍生了基于软件的tndp研究。
吴亮 [37] 从单条公交线路和整体公交线网两方面建立了基于transcad软件阐述了公交线路优化的具体方法,提出了适用于transcad软件的公交线网优化方法;对道路网、交通小区和公交线路系统进行了深入研究,细致研究了公交客流需求的预测方法和基本原理,对各个阶段的交通规划模型进行了详细介绍,对比,并进行了具体应用,利用实例建立公交线路系统,录入了大量基础数据。
李发宗等 [38] 对transcad中的交通分配模型的分配方法进行比较分析,选择其中的用户平衡分配模型来对某城市的交通流量进行分配, 为我们进行城市交通流分配的应用提供了一种实际可行的方法。
马骥、裴玉龙 [39] 对于模型选择的关键问题,尤其对交通需求预测中的交通分布、交通分配两步骤的模型进行详细探讨,最后给出应用transcad软件对大庆市市区交通需求进行预测的算例,得到与实际调查相符的交通量分配结果 [39] 。
基金项目
山东省自然科学基金(zr2018ma006),山东省研究生教育创新计划项目(sdyy15129),山东省研究生导师指导能力提升项目(sdyy17009)。
notes
*通讯作者。