1. 引言
此次调查问卷主要对大学生对课表时间、地点、课程安排等各方因素进行调查 [1] [2]。调查采取随机抽样形式。本次调查共发出问卷139份,实际回收的有效问卷139份,有效率为100%,在不同的年级中大一占15%,大二占50%,大三占20%,大四占8%,研究生占7%,分布情况见图1,在不同专业属性中理科占40%,工科占21%,文科占27%,其他占12%,分布情况见图2。由于在此次抽样调查中,充分考虑了样本的代表性,因此此次调查较为客观地反映了当前大学生对排课的需求。为方便学生答题,问卷均采用选择题形式,分为单选和多选。
2. 以层次分析法对排课系统进行分析
通过资料收集、平时的上课经验以及相关的研究报告,我们先确定了目前影响高校排课合理性的四个因素:上课时间、上课频率、课程分布和教室远近,即四个评价准则 [3]。其次,以这四个要素为依据,我们设计了专门的调查问卷。最后,通过问卷调查的结果,并结合专家打分的结果,确定这四个要素的比重 [4]。最后,利用层次分析法得出在上述四个因素的影响下合理的课表。
2.1. 建立层次分析模型
根据上课时间、上课频率、课程分布和教室远近四个评价准则建立层次分析模型,如图3。
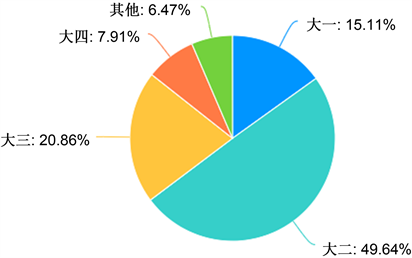
. grade distribution map
图1. 年级分布图
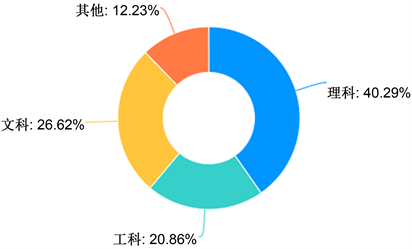
. professional distribution map
图2. 专业分布图
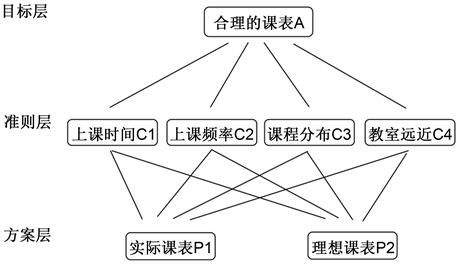
. analytic hierarchy model
图3. 层次分析模型
2.2. 构造准则层对目标层的成对比较阵
邀请四位专家对c1、c2、c3、c4四个因素进行打分,加权平均后得到准则层相对于目标层的成对比较阵,如下:
对a矩阵做列向量归一化得
再对其做行和归一化得
则
由于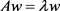 得:
得:
2.3. 确定准则层对目标层的权向量
由于准则层对目标层的成对比较阵为一致的,因此准则层对目标层的权向量为:
2.4. 一致性检验
一致性指标
随机一致性指标ri = 0.9 (查表)。
一致性比率cr = 0.0238/0.9 = 0.0264 < 0.1。
通过一致性检验 [5]。
3. 以模糊评价法对排课系统进行分析
3.1. 模糊评价法基本步骤
3.1.1. 简介
模糊综合评价是以模糊数学为基础,应用模糊关系合成的原理,将一些边界不清,不易定量的因素定量化,进行综合评价的一种方法。例如“年轻”与“年老”、“高”与“矮”、“欢迎”与“不欢迎”等等。凡是涉及到模糊概念的现象,即称之为模糊现象。
模糊综合评价法的特点在于,评价对象逐个进行,对评价对象有唯一的评价值,不受评价对象所处对象集合的影响。
模糊综合评价的数学模型分为一级模型和多级模型,一级模型也称为单层次评价模型。首先对影响总目标的多个因素列出构成一个因素集(评价指标),同时建立评价集(评价等级)。然后进行单因素评判,根据评价集对因素集中每一个因素进行模糊判断,确定每个因素在评价集中对各个评价等级的隶属度的大小,构成模糊矩阵。对因素集中每个因素赋予不同的权重,构成权重向量,从而得出最后的评判结果。
3.1.2. 模糊综合评价法优缺点
优点:
模糊综合评价法通过精确的数字手段处理模糊的评价对象,数学模型简单,容易掌握;
可以将不完全信息、不确定信息转化为模糊概念,使定性问题定量化,提高评估的准确性 [6];
评价结果可以是一组向量,也可以是一个点值,包含的信息比较丰富。
缺点:
模糊关系矩阵、权重、算子的选择都有一定的主观性;
隶属函数的确定还没有明确的且系统的方法;
当同一指标层级的指标个数较多时,会导致权系数较小,出现超模糊现象,分辨率较差,造成评估失败。
针对一级模型,模糊评价法的运用分为以下几个过程:
3.1.3. 确定评价对象的因素集
因素集是影响评价对象的各种因素所组成的一个普通集合。
表示因素集,其中ui为各影响因素。
3.1.4. 建立评价集
评价集是专家用自己的经验和知识对项目因素对象可能做出的各种总的评价结果所组成的集合,设为
,其中vi表示各种可能的评价结果。
3.1.5. 建立模糊关系矩阵
模糊关系矩阵即建立从u到v的模糊关系
,利用模糊统计方法,由若干专家对各因素rij进行评价,则rij = (对v中某一因素,专家划分某一档次的人数)/评审专家人数
得到模糊关系矩阵
3.1.6. 确定权重集
权重集反应了因素集中各因素不同的重要程度,一般通过各个因素
赋予一相应的权数
,这些权数所组成的集合成为因素权重集,简称权重集,设为
。权重的确定一般由人们根据实际问题的需要主观断定,也可按确定隶属度的方法加以确定。
3.1.7. 模糊综合评判
根据模糊综合评判数学模型进行模糊合成,就可得出综合评价结果—模糊综合评价集b为:
“*”运算符表示将对应元素两两比较先取小,然后再在所在结
果中取较大值。若b中各元素的总和不为1,需要对b中每个元素分别除以各元素的总和,得到归一化的矩阵b作为综合评价的结果。
3.2. 问卷分析
下面我就用问卷中的数据进行模糊综合评价法的应用:由于考虑课表的上课时间、上课频率、课程分布、教室远近这四个因素,对这四个评价因素的评价结果分为很好、好、一般、不好,因此模糊矩阵r为一个四阶矩阵 [7]。
本次问卷调查,我们共回收了十份有效问卷。通过对问卷的分析得到教师对四个因素的评价。
对上课时间的评价参考问卷的第2、7、8、9题,所以采取了每个问题分别建立评价集的方法,最后将每题的打分取平均并标准化。对问题2,问卷结果显示所有教师都不希望在体育课后授课,课表符合要求,评价都为很好,因此根据问题2,对上课时间的评价为
。对问题7,问卷结果显示有六名教师非常愿意在早上八点授课,两名教师可以接受,还有两名教师无所谓,由于课表在早上八点都有课,因此根据问题7,对上课时间的评价为
。对问题8,问卷结果显示有七名教师希望将课程安排在早上第一节,还有三名教师希望安排在早上第二节,这说明教师都希望课程安排在上午,因此可以直接根据课程所处的时间对上课时间进行评价,即第一、二、三、四节的评价依次为很好、好、一般、不好。结合课表,对于问题8,我们对上课时间的评价为
。对问题9,问卷结果显示,有一位教师完全接受在饭点安排课程,一位教师可以接受,三名教师表示无所谓,四名教师不接受,还有一名教师完全不接受,结合课表来看,中午都安排了课程,所以可以直接根据问卷结果得到对上课时间的评价,其中完全接受对应的评价为很好,接受对应好,无所谓对应一般,不接受和完全不接受都视为不好,因此对于问题9,我们对上课时间的评价为
。最后,将这四个评价取平均并标准化,就得出了我们对这份课表上课时间这个因素的评价,为
。
对上课频率的评价参考问卷的第3题。问卷结果显示有三名教师认为同一课程间隔一天效果较好,有六名认为间隔两天较好,还有一位教师认为间隔三天较好,说明大部分教师认为间隔两天较好,因此对于间隔两天的课程的评价为很好,间隔一天为好,间隔三天为一般,结合课表来看,间隔一天的有一门课,间隔两天的有四门课,没有间隔三天的课程,所以只需考虑很好与好两个评价等级。根据课表,很好的课程与好的课程分别占4/5和1/5,再乘上问卷中相应的比例,再标准化,从而得到对上课频率这一因素的评价
。对课程分布的评价参考问卷的第五题。问卷结果显示有九名教师希望课程集中在上午,还有一名教师希望集中在几天上午。课表中出周二的其他四天,课程都集中在上午,因此这四天评价为好,占4/5,周二评价为不好,再结合问卷中各个选项的比例并标准化,得出对课程分布这一因素的评价为
。
对教室远近的评价参考问卷的第十题。问卷结果显示有六名教师非常希望把上午或下午的两节课安排在同一间教室,有两名教师比较喜欢安排在同一间,还有两名教师表示无所谓。结果表明大部分教师希望不换教室,因此对换教室的课程评价为不好。课表中没有课程是在同一间教室的,因此结合问卷,对这份课表评价为不好的教师占80%,一般的占20%,从而对教室远近这一因素的评价为
。
因此,我们得到模糊举证r为
。
通过专家打分,我们得出评价集
,归一化处理后得到
。由公式
得,
,归一化后得
。最后我们得出了
综合模糊评果
。
3.3. 模糊评价法结论
计算结果表明,教师对课程安排评价为很好的有25%,评价好的为17%,评价一般的为20%,评价不好的为18%。根据最大隶属度原则,对课程安排的综合评价为很好。
4. 本文结论
我们此次研究的目的在于为学生和教师都提供更加合理的课表,从两次问卷调查结果来看,学生和教师都对课表安排有着一定的诉求,并且存在着分歧。研究表明,排课时应更加注重课程的时间安排,上午以及一周中的中间时间可以尽量安排重要的课程;而饭点、体育课后、周末等敏感时间点,尽量不要安排课程。但是实际上,学生的课表与教师的课表是不同的,学生的课表课程种类多、频率低,此时还要注意课程的教室安排,相邻的课程尽量安排在同一或相邻教室;教师的课表课程种类较少而频率较高,此时应该注意每天的上课量尽量平均且合理。
本文中所举课表从学生与教师的角度分析结果都是较为合理的,但该研究结论有助于改进课表的合理性,使之评价更高。
基金项目
江苏高校品牌专业建设工程资助项目(数学与应用数学,ppzy2015b109);扬州大学大学生学术科技创新基金项目(批准号:x20190216)。
notes
*通讯作者。