1. 引言
c4烯烃在化工和医药产品中有广泛应用,乙醇可以用来生产制备c4烯烃。在制备的过程中,催化剂组合和温度以及乙醇浓度的选择对c4烯烃的选择性和乙醇转化率有影响,所以研究乙醇催化偶合制备c4烯烃的工艺条件十分重要,具体来说就是要建立催化剂组合、温度和乙醇浓度对乙醇转化率和c4烯烃选择性的关系建模并在此基础上寻找最佳的催化剂组合、温度及乙醇浓度使得c4烯烃收率最大。这方面的研究以2021年数学建模高教社杯b题的形式得到广泛关注。目前已发表的成果中,吕绍沛主要应用化学实验的研究方法对乙醇偶合制备丁醇及c4烯烃的工艺条件进行研究,其在数据处理和分析方面没有作过多的研究 [1]。李明等人只单独分析了不同催化剂组合下对乙醇转化率和c4烯烃的回归拟合分析,没有建立工艺条件对乙醇转化率及c4烯烃选择性的整体关系建模 [2]。李韶伟等人通过灰色关联法分析了乙醇转化率和c4烯烃选择性的影响因素,又采用指数回归单独分析温度的影响,然后运用高斯回归分析寻找最佳工艺条件,在影响因素的探究和工艺条件的优化上不具备分析的连贯性 [3]。本文考虑到所研究对象样本个数较少、数据维度较大以及其存在的非线性关系,将核偏最小二乘回归kplsr (kernel partial least-squares regression)引入到乙醇偶合制备c4烯烃的工艺条件对乙醇转化率、c4烯烃选择性的关系建模中,并对建模结果做了交叉检验,和一般的偏最小二乘回归plsr (partial least-squares regression)作了复测系数比较,发现模型具有相当的可靠性。在此基础上,结合了遗传算法ga (genetic algorithms),模拟退火算法sa (simulated annealing),粒子群算法pso (particle swarm optimization),提出一种混合优化算法,即基于遗传算法的模拟退火粒子群算法gapa (genetic annealing particle algorithms),运用该算法对核偏最小二乘的建模结果作优化问题,从而找到最佳的工艺条件,使得c4烯烃收率最高,并和ga、sa、pso进行比较,在收敛速度和准确性上具有明显优势。
2. 研究方法
2.1. 偏最小二乘回归
偏最小二乘回归(partial least-squares regression)是一种先进的多元分析方法。它于1983年由伍德和阿巴诺等人首次提出,主要用来解决多元回归分析中的变量多重相关性或解释变量多于样本等实际问题。它提供了多对多的数据分析方法,其集中了主成分分析,典型相关分析,线性回归分析方法的特点,在针对变量较多且具有多重线性相关性,而样本量较少时具有相当的优势。下面给出偏最小二乘回归的计算方法推导。
记x数据标准化后的数据矩阵
,y经标准化处理后的数据矩阵记为
。
第一步:记
是
的第一个成分,
,
是
的第一个轴,它是一个单位向量,也就是
。记
是
的第一个成分,
,
是
的第一个轴,它是一个单位向量,也就是
。如果需要
和
能分别很好地表示x和y中的数据变异信息,根据主成分分析原理,有
另一方面,因为回归建模的要求
对
有最大的解释能力,根据典型相关原理,
对
的相关度应该达到最大值,即
因此综合起来,在偏最小二乘回归中要求
与
的协方差为最大值,即
也就是在
和
的约束条件下,去求
的最大值,由拉格朗日算法,记
对s分别求
,
,
和
的偏导,并令其为0,得到
由上式可得
可见
是矩阵
的特征向量,对应的特征值为
其中
是目标函数值,它要求取最大值,于是
是对应于
矩阵最大特征值的单位特征向量。而
是对应于矩阵
最大特征值
的单位特征向量。求得
和
后可得成分
之后求
和
对
和
的三个回归方程
其中
分别是三个回归方程的残差矩阵而回归系数向量是
第二步:用残差矩阵
和
取代
和
,然后求第二个轴
和
及第二个成分
和
,有
是对应于矩阵
最大特征值
的特征向量,
是对应于矩阵
最大特征值的特征向量,计算回归系数
进而有回归方程
如此计算下去,如果x的秩是a,则有
由于
均可表示成
的线性组合,故上式还可以写成
关于
的回归方程如下:
是残差矩阵的第k列 [4]。
2.2. 核函数
核函数(kernel function)是一种曲线光滑拟合技术,核函数概念起源于核估计量(kernel estimator)而核估计是近似估计数据总体的概率密度函数的方法。非参数概率密度估计方法的主要思想是:设
是从未知概率密度函数
的总体中抽出的样本点。对任意指定的x,依据这些样本点估计该点上的密度
的值。常用的核函数有均匀核函数,二次权重核函数,高斯核函数等。
2.3. 核偏最小二乘回归
核偏最小二乘是一种通过核函数将变量空间变换到特征空间,再利用偏最小二乘回归的线性方法求解回归系数的非线性回归方法 [5]。其建模一般方法步骤如下
第一步:对自变量每一维进行核函数变换。
第二步:将因变量及新的自变量进行标准化处理。
第三步:对处理后数据进行偏最小二乘求参。
2.4. 遗传算法
遗传算法(genetic algorithms)是一种基于自然选择原理和自然遗传机制的搜索算法,它是模拟自然界中的生命进化机制,在人工系统中实现特定目标的优化。遗传算法的实质是通过群体搜索技术,根据使者生存的原则逐代进化,最终得到最优解或准最优解。其主要实现方法为:产生初始化群体,求解每一个个体的适应度,选择优良个体、被选出的优良个体两两配对,通过随机交叉其染色体的基因并随机变异某些染色体基因生成下一代群体,按此方法使群体逐代进化,直到满足终止条件为止。不同的群体规模m、交叉概率pc、变异概率pm、进化终止条件,将会对计算结果的迭代次数和精度产生较大影响,需要进行多次实验以获得性能较好的一组参数 [6]。
2.5. 模拟退火算法
模拟退火算法(simulated annealing)对自然界中物体温度下降过程进行模拟,是一种全局优化算法。在高温中,物体粒子进行自由运动和重新排列,随着温度下降,粒子的运动能量逐渐下降,最终形成处于低能状态的晶体。其主要实现方法为:首先给定一个初始温度
和该优化问题的初始解
,并由
产生一个新解
,是否接受
为新解
依赖如下概率:
(1)
在温度
下,经过多次随机产生新解并依概率p选择后,降低温度
,得到
。在
下重复上述过程。经过不断寻找新解和缓慢降温的交替过程。最终得对该问题的寻优结果 [7]。
2.6. 粒子群算法
粒子群优化算法(particle swarm optimization, pso)是一种初始化为一组随机解,通过迭代搜寻最优解的随机搜索优化算法。设在一个n维的目标空间内,有m个粒子组成了一个群体,其中第i个粒子的位置为
,
,每个粒子的速度为
,
,随着粒子的速度和位置不断更新,全局最优解和局部最优解不断迭代更新,根据每个粒子的速度和位置计算目标函数当前的适应值,并通过迭代更新找到最优解。其中,速度和位置更新公式为:
(2)
式中,
为粒子i在t时刻的速度;
为粒子i在
时刻的速度;
为粒子i在t时刻的位置;
为粒子i在
时刻的位置;
为惯性权重;
和
为学习因子;
和
为在
范围内取值的随机数;gbest为局部最优位置;pbest为全局最优位置 [8]。
2.7. 基于遗传算法的模拟退火粒子群算法
粒子群算法具有全局搜索能力,但容易陷入局部最优解。遗传算法的收敛速度较快且同样具有全局搜索能力,而模拟退火算法可以以一定概率接受较差的解,进而提升算法摆脱局部最优解的能力。为此本算法将三种进行结合,在遗传算法的交叉互换与变异操作后引入对每个个体粒子的速度与位置进行更新,其中位置更新以模拟退火算法中的接受概率进行选择是否新位置。最终实现一种收敛速度快,不易陷入局部最优解且寻优精度较高的算法。算法流程图见图1所示,主要分为遗传算法、模拟退火算法、粒子群算法三大部分,其具体实现步骤为:
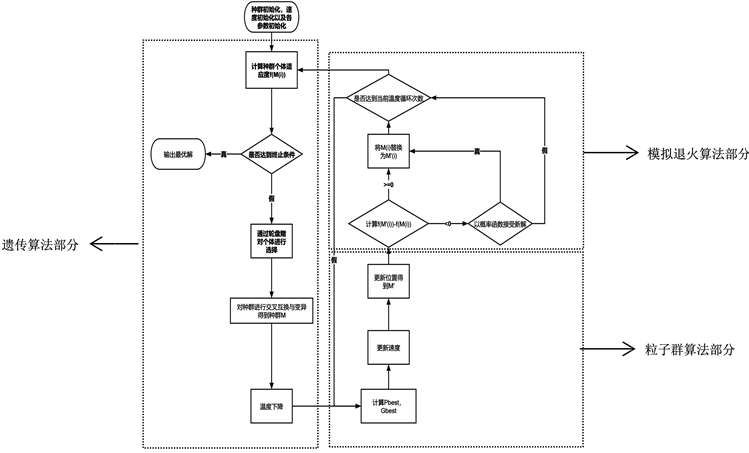
. block diagram of genetic annealing particle algorithms
图1. 基于遗传算法的模拟退火粒子群算法流程框图
(1) 设定算法迭代次数n、种群的规模m、种群交叉率pc、变异率pm、初始温度ti、温度下降率pt、同一温度下迭代次数nt、惯性权重ω、学习因子c1和c2、并随机生成个体的速度矩阵vi。
(2) 依据适应度函数对种群m内每个个体计算适应度。
(3) 依据个体适应度进行轮盘赌,保留适应度更高的个体,并对这些个体进行交叉互换与变异,得到更新后的种群m。
(4) 依据pt使温度ti下降。
(5) 确定gbest,pbest:计算种群中每个个体的适应度函数值作为待定gbest并与个体前代的gbest进行对比,取较大的作为本代gbest,所有个体中gbest中的最大值即为pbest。
(6) 依据式(2)对vi进行更新,并按照式(1)作为接受概率对m进行更新。
(7) 重复nt次步骤(5)和步骤(6)。
(8) 判断是否满足终止条件,不满足则从步骤(2)开始继续进行循环。
3. 基于核偏最小二乘回归的乙醇转化率及c4烯烃选择性建模
3.1. 数据处理
本文采用2021高教社杯b题的附件数据并作处理如下。对实验数据观察发现,只有一组含有石英砂而其他为hap,故直接剔除该组数据。另外发现装料方式对实验的影响较小,故本文只分析催化剂组合,温度及乙醇浓度对乙醇转化率和c4烯烃选择性的影响。这里本文将催化剂组合的影响拆分为四个变量为co的负载量w,co/sio2和hap的装料比cr,co/sio2和hap的质量和cs,另外两个实验影响因素是乙醇浓度e加上温度自变量t,因变量为乙醇转化率r和c4烯烃选择性s。最终得到98组样本,每组样本包含了7个维度的信息。
3.2. 核偏最小二乘建模
由于问题的小样本容量特征及其多变量特征,再考虑其非线性的因素,故采用核偏最小二乘回归的方法来研究催化剂组合,乙醇浓度以及温度和乙醇转化率,c4烯烃选择性的关系。下面给出建模的具体步骤。
(1) 利用高斯函数对自变量数据进行核变换,得到核(gram)矩阵
,其中高斯函数为
其中
,r取5,m自变量数据维度取5,
为数据总体标准差 [9]。
(2) 对变换后数据进行标准化处理。
(3) 分别提取自变量组和因变量组提取第一成分
,且使相关性最大。
(4) 建立r,s对
的回归,和
对
的回归。
(5) 用残差阵代替原回归阵,重复步骤234,直到满足回归精度为止。
(6) 对模型进行交叉有效性检验。
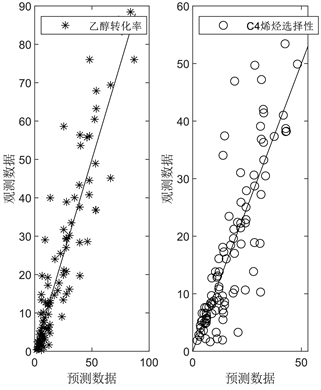
为了可视化建模结果并同时考察回归精度,本文绘制了样本点的观测值和预测值比较图,并将其和一般偏最小二乘回归得到的结果进行比较。
图2的结果直观地展示了核偏最小二乘回归和偏最小二乘回归两种模型的预测效果,其中(a)为核偏最小二乘的结果,(b)为偏最小二乘的结果,显然核偏最小二乘回归所得到的数据相较于偏最小二乘回归的结果更均匀更集中分布于斜线y = x两侧,也就说明了在对不同催化剂组合,温度和乙醇浓度对乙醇偶合制备c4烯烃下乙醇转化率和c4烯烃选择性的关系建模上,核偏最小二乘回归的模型精度优于偏最小二乘回归的模型精度。
3.3. 变量权重分析
为了进一步更直观地观测各个变量对解释乙醇转化率r和c4烯烃选择性s的边际作用,绘制了在数据经过核函数变换后其对r和s的回归系数直方图如图3所示。
图3中左侧(1) 5条分别为t,w,cr,cs,e对r的系数,右侧(2) 5条分别为t,w,cr,cs,e对s的系数,从中可以看出温度t和乙醇浓度e对r的影响较大,且前者为正影响而后者为负影响。温度t,由催化剂组合分出的两个变量cr,cs,乙醇浓度e对s都有不小的影响,前两者为正影响,后两者为负影响。
 (a)
(a)  (b)
(b)
. comparison chart of observed and predicted values
图2. 观测值和预测值比较图
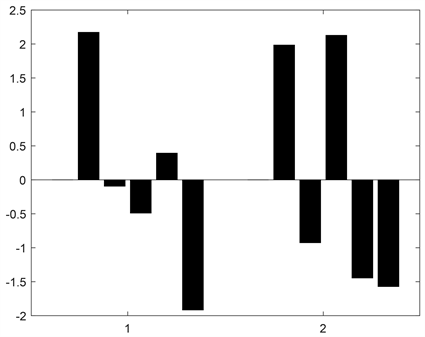
. histogram of regression coefficients
图3. 回归系数直方图
3.4. 复测定系数分析
为了对模型的有效性进行定量化的分析,分别对核偏最小二乘回归和偏最小二乘回归得到的数据做复测定系数,结果如表1所示。
复测定系数是拟合数据的变异平方和与原始数据的变异平方和的比值,它反映了回归方程对原始数据的拟合程度,由表1可知建模的结果具有相当的准确性,且核偏最小二乘方法优于线性的偏最小二乘得到的结果。
. coefficient of complex determination
表1. 复测定系数
4. 混合优化求解
4.1. 问题说明
基于前面核偏最小二乘得到的催化剂组合,温度,乙醇浓度对乙醇转化率r和c4烯烃选择性s的关系,将r和s得到结果相乘得到c4收率y对催化剂组合,乙醇浓度和温度的关系,以此作为优化目标,从而将寻找最佳工艺条件的问题转化为使得y最大的单目标优化。
4.2. 具体步骤和结果
利用python实现混合优化算法,即基于遗传算法的模拟退火粒子群算法。经过多次试验得到具体参数设置如下:迭代次数n = 80、规模m = 150、种群交叉率pc = 0.5、变异率pm = 0.05、初始温度ti = 75、温度下降率pt = 0.8、同一温度下迭代次数nt = 5、惯性权重ω = 0.8、学习因子c1 = 1和c2 = 2。将c4收率y与变量t,w,cr,cs,e的关系作为求解目标分别带入基于遗传算法的模拟退火粒子群算法(gapa)、模拟退火算法(sa)、遗传算法(ga)以及粒子群算法(pso)。结果如图4,表2所示。
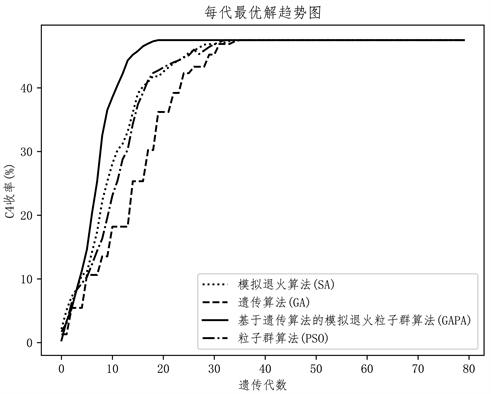
. comparison of the optimization process of each algorithm
图4. 各算法优化过程对比
从图4中可以看出,基于遗传算法的模拟退火粒子群算法求解c4收率问题的迭代次数明显少于其余三种算法。这体现了此算法收敛速度快的特性,同时在准确性方面仍具有较高的精度。由表2可见,在t = 450,w = 0.5,r = 2.03,s = 400,e = 0.3的条件下,可得到c4收率最大值为47.5%。
. comparison of optimization results by each algorithm
表2. 各算法优化结果对比
5. 结论
c4烯烃在化工和医药产品中有广泛应用,这使得探究乙醇偶合制备c4烯烃的工艺条件具有重要意义,本文利用核偏最小二乘建立工艺条件对乙醇转化率和c4烯烃选择性的关系,虽然模型精度较偏最小二乘有所提高,但通过复测定系数分析发现对c4烯烃选择性的模型精度稍差,需要提高。为了探究最佳工艺条件,将乙醇转化率和c4烯烃选择性的乘积即c4收率作为单目标,利用基于遗传算法的模拟退火粒子群算法进行优化,发现其相较于单独的遗传算法,模拟退火算法,粒子群算法在收敛速度和准确性上有所提高,但由于算法需要设置的参数较多,这不利于算法的普适性,需要改进。