1. 引言
随着经济和社会快速发展,城市交通的拥堵问题日益严重。交通的实时动态管理与交通道路控制已经成为必不可少的研究,交通道路控制的前提是做好短时交通量预测和交通信息采集等,来提高智能交通系统的运行效率 [1]。做好交通控制和诱导系统必须要做好短时交通量预测,短时交通量预测是以几分钟为数据单元进行时间序列的分析预测,滚动实时预测未来短时段的交通量。通过短时交通流量预测为交通管理部门提供参考,为交通的实时动态管理提供更好的依据 [2]。
交通流量短时预测方法众多,大部分学者采用机器学习和深度学习方法进行预测,提高短时交通道路流量的预测精度,同时时间序列模型也被广泛运用,例如arima (autoregressive integrated moving average)模型。arima时间序列模型考虑了序列的有序性、时间性和随机因素的不确定性所造成的干扰因素,选用数据并不受约束与限制,适用范围广,应用性强,而且短期预测效果较好 [3]。刘学刚等人同样采用arima模型对交通道路进行短时预测,并且表明在短时交易量预测时有很大的应用价值 [4]。徐翠翠提出基于arima模型的城市道路交叉口交通流预测,提取现场每天24 h交通流数据,分析不同时间序列的交通流特征 [5]。机器学习中svm (support vector machine)模型有着分类作用与非线性拟合功能,可以准确地拟合交通流量序列中的非线性变化特征 [6]。最近几年混合模型相比于单一模型更受学者青睐,有学者采用时间序列模型与机器学习模型混合来预测交通流量 [7]。大部分学者采用svm模型与神经网络组合预测交通流,也有部分学者采用优化的svm模型预测交通流。李媛媛在空间重构基础上分析混沌交通时间序列,采用svm相同原理研究最小二乘支持向量机,并应用于智能交通数据作短期预测 [8]。余涛分析了在较少数据集条件下,运用svm模型具有更好的预测效果,因此在较大数据集条件下采用svm模型与bp神经网络组合获得更好的预测效果 [9]。何祖杰等人采用改进灰狼算法优化支持向量机来预测智能交通流,并通过实证数据与粒子群算法进行对比,结果表明改进灰狼算法优化支持向量机具有鲁棒性与泛化能力 [10]。曾宪堂等人总结了不同文献短期预测交通流模型,将arima、knn、svm短期预测模型应用于高速公路,并进行比较 [11]。
城市交通拥堵状况与预测交通流分析一直是交通领域学者研究的热点话题,短期交通流预测能更好地描述某时段或某时刻的交通状态,因此本文采用贵州省贵阳市交通流量数据进行短期预测。本文采用arima与svm模型组合,使用arima模型,能够很好地刻画交通流量序列中的线性变化特征,但其对非线性变化特征的描述会产生一定的误差,然而svm模型可出色地拟合交通流量中非线性变化特征。最后使用平均绝对误差与平均百分比误差对结果进行分析。
2. 相关工作
2.1. arima模型
arima模型可分为自回归(autoregressive, ar)模型、滑动平均(moving average, ma)模型和arima(p, d, q)。滞后项为p阶的ar模型记为ar(p),ar(p)模型如下公式(1)所示:
(1)
其中,c为常数,
是ar(p)模型的自回归系数;
为白噪声序列,即随机误差项;
是时间序列t时刻的值,即
是时间序列
的滞后序列,即数据的自变量。滞后项为q阶的ma模型记为ma(q),ma(q)模型如下公式(2)所示。
(2)
其中,c为常数,
是ma(q)模型的自回归系数;
为白噪声序列,即随机误差项;
是时间序列t时刻的值,即数据的因变量。
ar模型可以刻画一个时间序列对过去自身的记忆,ma模型可以刻画一个时间序列对过去冲击的记忆。如果一个时间序列的变化规律中不仅包含了对过去状态的记忆,还包含了对过去冲击的记忆,则此时间序列的变化规律可以被arma模型捕获,滞后项分别为(p, q)的arma模型 [12]。arma模型如下公式(3)所示:
(3)
其中,
是t时刻样本序列值;
是服从高斯分布的白噪声序列;
是自回归系数;
为移动平均系数,其他为模型的约束条件。在arima模型中若q为0,则该模型arima(p, 0)退化为ar(p)。若p为0,则该模型arima(p, q)退化为ma(q)。
若一个时间序列是非平稳的,则不能直接用arma模型进行拟合(容易出现伪回归),此时必须对此时间序列进行平稳化处理。差分方法是平稳化时间序列最常用的一种方法,若一个非平稳时间序列经过d次差分后平稳,则依据此时间序列构建的arma(p, q)模型称为arma(p, d, q)模型 [13]。
2.2. svm模型
svm (support vector machine)模型具有很好的分类和拟合能力,通过使用空间转化,将非线性问题变成线性问题,从而可以解决高维非线性问题,同时可以避免局部较小问题 [14]。svm模型的基本思想是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
设有一训练数据样本集为
,其中
为n维输入向量,
为相应的期望输出值。svm回归估计函数如下公式(4)所示:
(4)
其中,
将输入向量映射到高维特征空间;w和b分别为权重和偏差,通过如下公式(5)和(6)求出:
(5)
(6)
上述权重和偏差求解式子中,c为正则化参数,用于控制经验误差和正则化项;
为不敏感损失函数,
为不敏感损失函数参数。
引入核函数
,结合拉格朗日函数和沃尔夫(wolfe)对偶理论,将权重与偏差求解公式转换为二次规划问题如下,公式(7):
(7)
其中,
和
为拉格朗日乘子,输入向量
对应的非零
和
为支持向量。因此,svm回归估计函数转换为回归函数如下公式(8)所示:
(8)
通过以上svm回归函数模型进行拟合和预测。
2.3. arima-svm模型构建
arima-svm模型建模思路为:通过arima模型预测交通道路流量序列中的线性特征,得到预测残差。由于残差中包含了交通道路流量的非线性特征,利用svm强大的非线性映射能力对残差进行修正并预测,最后将线性预测结果和残差修正结果进行组合,得到交通道路流量序列的预测值。
arima-svm模型短时预测交通道路流量的建模步骤如下:
步骤1:白噪声检验。采用q统计量检验以及自相关函数和偏自相关函数判断是否为白噪声序列。
步骤2:序列的平稳性检验以及平稳化处理。序列平稳性采用单位根和序列相关图判断,如果为平稳序列,则可以构建arima模型;如果为非平稳序列,则序列需进行d阶差分,差分后为平稳序列才可构建arima模型。
步骤3:模型识别与定阶。通过自相关系数图和偏自相关系数图的截尾性与拖尾性进行模型识别,确定采用时间序列ar,ma,arima其中一个模型。模型定阶同样根据自相关系数图和偏自相关系数图以及差分次数初步确定p,d,q的值。选择多组不同阶数模型进行拟合莫模型,比较aic准则,确定最优p,d,q的值。
步骤4:参数估计与检验。参数估计采用最大似然估计法进行估计,模型检验残差是否为白噪声序列。
步骤5:arima模型预测。通过构建的arima模型预测后10期预测值,并获得残差序列。
步骤6:svm模型构建并残差修正。设定svm核函数,将残差序列输入svm,采用交叉验证法确定svm的最佳参数值,从而构建svm模型。根据svm预测残差序列,获得残差预测值。
步骤7:组合预测值。将arima模型的预测值与svm的残差预测值进行加和,得到最终交通道路流量的后10期预测值。
3. 实例验证
本文采用的数据是贵州省贵阳市观山湖区长岭北路与东林寺路交叉口的真实交通流量数据,如下图1所示。采用2021年3月1日至2021年3月16日连续16天的短时交通流量数据,数据采用5 min为时间间隔统计交通流量q。将2021年3月1日至2021年3月15日作为训练集,2021年3月16日前10个时间序列点作为测试集。将训练集可视化,可得到长岭北路与东林寺路交叉口序列图,如下图2所示。
. intersection of changling north road and donglinsi road
图1. 长岭北路与东林寺路交叉口
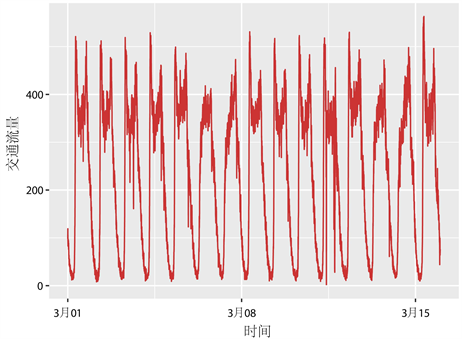
. sequence diagram of daily traffic flow at the intersection of changling north road and donglinsi road
图2. 长岭北路与东林寺路交叉口日流量序列图
3.1. arima-svm模型构建与预测
在模型构建与预测之前,对训练序列数据进行时间序列分解,分解结果如下图3所示。从图中可看出序列具有规律的周期性以及带有一定的趋势性和波动。
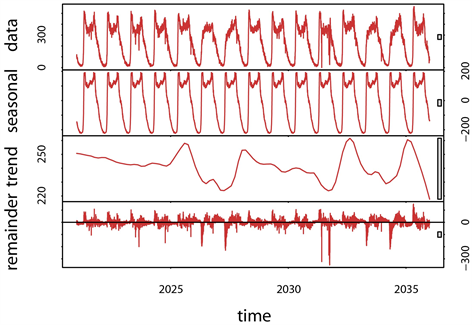
. time series decomposition plot
图3. 时间序列分解图
从时间序列分解和序列图来看,该序列的在不同值附件有小范围波动,可以大致判断该序列不是一个平稳序列。使用自相关函数和偏自相关函数进一步判断是否为非平稳序列,自相关函数图和偏自相关函数图如下图4所示,该序列的自相关系数没有迅速下降为0,也没有收敛到0的2倍标准差范围内,可以判断该时间序列不是平稳序列。进一步对该时间序列进行单位根检验和白噪声检验,单位根检验的p值和滞后6阶的纯随机性检验的p值分别为0.01、0.000022,可见该序列为非白噪声序列。
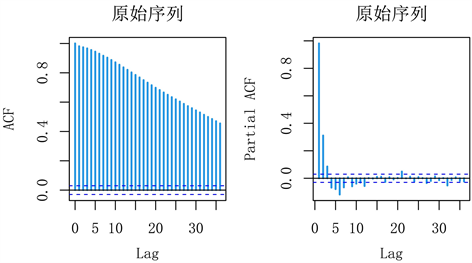
. time series acf and pacf
图4. 原始序列自相关系数图和偏自相关系数图
从以上方法判断该时间序列为非平稳序列,将该序列进行一次差分,并对差分后的序列进行可视化,得到差分后序列图,如下图5所示,比原序列更平稳。将差分后序列作自相关系数检验,从自相关系数图上看,该差分后序列平稳,自相关系数图和偏自相关系数图如下图6所示。从自相关系数图看出,差分后序列一阶后基本上衰减为0,到6阶之后都在0的2倍标准差范围内,具有拖尾性质。从偏自相关系数来看,差分后序列6阶之后大部分衰减为0,具有拖尾性质。
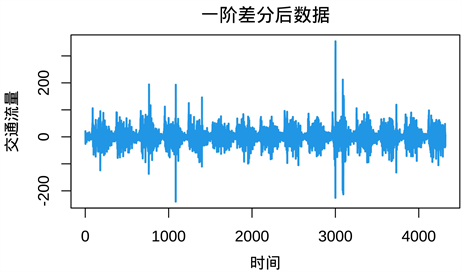
. sequence diagram after one difference
图5. 一次差分后序列图
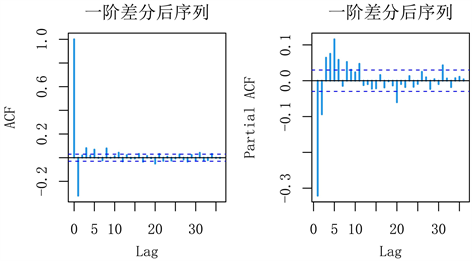
. acf and pacf after first difference
图6. 一次差分后自相关系数图和偏自相关系数图
根据一次差分后自相关系数和偏自相关系数对模型进行识别与定阶,从以上分析来看对该时间构建arima模型,并进行初步定阶为(6, 1, 6)。将定阶的附近取值同样构建模型,并使用aic准则选择一个最优arima模型,定阶过程如下表1所示。从表中的aic准则可得出,arima(5, 1, 6)时aic值最小,为40914.99,因此最终选择时间序列模型为arima(5, 1, 6)。
arima(5, 1, 6)模型构建之后进行模型诊断和残差检验,检验图如下图7所示。该差分序列的残差大致都在一个值附近波动,并且残差的自相关系数图在开始就衰减为0,ljung-box检验的p值都在0.05以上,说明模型构建合适。接着检验残差是否相关以及满足正态分布,box.test的p值为0.8599,证明残差还存在相关性。残差是否满足正态分布的直方图如下图8所示,并不满足0均值的正态分布。qq图如下图9所示,也证明了残差还有非线性特征未提取。将构建的arima(5, 1, 6)模型进行滞后10期预测,可得到后10期的预测值。
. sequence model construction selection criteria
表1. 序列模型构建选择准则
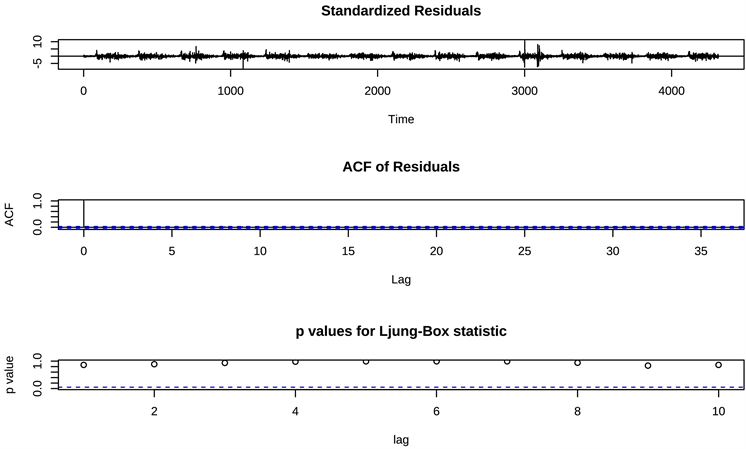
. model diagnostics and residuals test plots
图7. 模型诊断和残差检验图
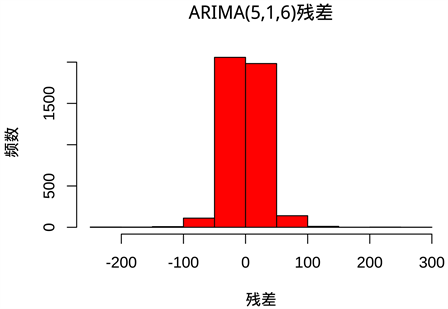
. residual histogram
图8. 残差直方图
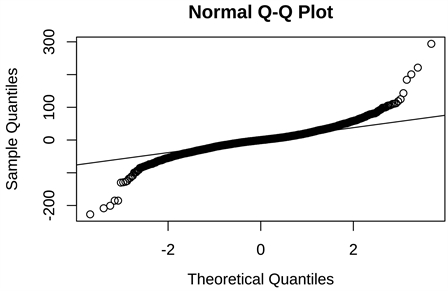
. residual qq plot
图9. 残差qq图
3.2. svm模型构建与预测
本文采用svm对arima模型的残差序列进行修正,将arima模型的训练序列的残差值作为输入,后10期的序列残差值作为输出。核函数主要有线性核函数、多项式核函数、径向基核函数、多层感知机核函数、傅里叶核函数、小波核函数、混合核函数等。本文基于研究数据选择径向基核函数,此核函数的参数较少,并且性能不受数据样本大小的影响 [15],其表达式如下:
(9)
其中,
为核参数。从svm回归函数可知,正则化参数c、不敏感损失函数
,不敏感损失函数参数
三个参数需要确定,此处采用5折交叉验证进行确定参数,可得均方误差分别为848.8907,736.8186,689.5426,745.7129,774.5315,选取最小均方误差所对应的参数。
3.3. 结果分析
本文的道路交通流量使用arima-svm模型进行预测,将序列后10期的预测值与2021年3月16日的0时0分至0时45分的真实值进行评价预测性能。此处采用平均绝对误差和平均百分比误差这2个指标进行评价,其平均绝对误差a和平均百分比误差p表达式分别如下:
其中,
和
分别表示长岭北路与东寺林路交叉口的真实值与预测值,平均绝对误差和平均百分比误差越小,则模型的预测精度越好。本文同时分别采用arima、svm、arima-svm三个模型预测交通流量,并采用平均绝对误差a和平均百分比误差p评价模型预测性能。
预测结果如下表2所示,arima模型预测线性部分的值与真实值在2021年3月16日的0时20分、0时25分、0时30分相比,预测值较大,其他时间点预测值与真实值之间相差不大。将arima模型预测的线性部分和svm模型预测的非线性部分进行加和,可得最终预测值。
. forecast result
表2. 预测结果
将预测结果使用评价预测性能指标即平均绝对误差a和平均百分比误差p,进行计算,可得平均绝对误差a为7.7,平均绝对误差不大,平均百分比误差p为12.7%,说明arima-svm混合模型预测效果较好。本文将arima、svm模型与arima-svm模型的预测性能作对比,如下表3所示。三种模型预测性能arima-svm最佳,其次是arima模型,最后是svm模型。
. model evaluation
表3. 模型评价
4. 结束语
本文采用arima-svm模型对贵阳市长岭北路与东寺林路交叉口交通流量进行预测,从预测结果来看,此模型预测结果理想,因此此模型作为短时预测效果较好。采用arima模型预测序列线性部分特征,svm模型对arima模型的残差进行修正并预测,并通过贵阳市长岭北路与东寺林路交叉口交通流量数据验证了模型的有效性。通过短时交通量预测未来时间点的交通流量,为交通管理部门提供思考与解决交通拥堵干预,有效地减少交警盲目出警与人力成本。