1. 前言
客观世界的许多现象和事物不仅仅是运动变化的,而且其运动变化的过程往往是连续的,比如环境温度、日月星空、江河湖海、岁月流逝、植物生长、物种变化等,这些连续不断发展变化的事物在量的方面反映就是函数的连续性,本文在讲解连续函数知识的概念的基础上,通过分析连续的内在本质和逻辑成因,释放函数连续性中蕴含的思想价值和德育基因,通过滴灌、漫灌渗透到知识体系中去。该探究为深入推进运筹学德育的实践进步提供了一种有效的阐释 [1] [2] [3]。
2. 教学实践———以函数的连续性为例
2.1. 函数连续性知识点及其数学思想解读
2.1.1. 函数连续性历史脉络
19世纪以前,数学家们对连续变量的理解和研究仍停留在几何和具象直观的视角。19世纪中叶,以柯西和维尔斯特拉斯为代表的数学家建立起了严格的极限理论之后,才对连续函数做出了严格的数学表述。因此可以说目前教材中有关函数连续性的描述产生过程也是数学家们连续不断探索的结果。
2.1.2. 函数连续性知识点
a) 增量的概念
设变量u从它的一个初值
变到终值
,则称终值
与初值
的差
为变量u的增量(改变量),记作
,即
b) 函数
的增量
设函数
在点
的某一领域内有有定义,当自变量x在
处取得增量
时,相应地,函数
从
变到
,则称
为函数
对应的增量(图1,图2所示)。
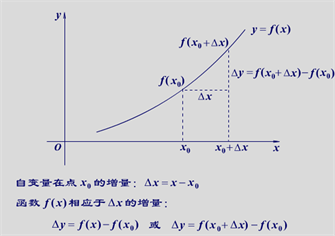
. when the increment of the independent variable is greater than zero
图1. 自变量的增量大于零时
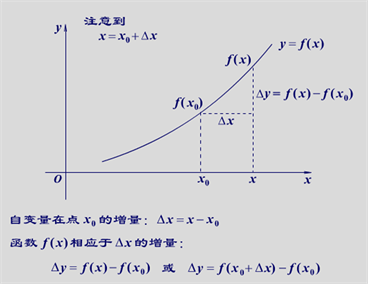
. when the increment of the independent variable is less than zero
图2. 自变量的增量小于零时
c) 连续函数的概念
连续的定义1 设函数
在点
的某一领域内有定义。如果当自变量在点
的增量
趋于零是,函数
对应的增量
也趋于零,即
或
则称函数
在点
处连续,
成为
的连续点。
连续的定义2 设函数
在点
的某一领域内有定义。如果函数
当
时的极限存在,且等于函数
在点
处的函数值
,即
则称函数函数
在点
处连续。
从定义1不难看出,
,
都是
时的无穷小量,或者可以说是定义是从无穷小量的角度出发给出了函数数
在点
处连续的概念。反观定义2,从函数在该点的极限和函数值的角度给出了一个较为简单的定义。尽管定义2是从定义1的基础上推导而来,但它给出了一个求极限的一类方法,即如果函数在某点是连续的,则自变量趋近该点的极限值等于该点的函数值。从定义1到定义2实际上就是运用普遍联系的观点,特别是转化的思想去认识,去解决的(从极限值到函数值)。
而后,从左右极限出发分别定义了左右连续的概念,并给出了函数在某点连续的充分必要条件。左、右连续的引入按照函数点连续的定义,若函数在一点连续,那么必须存在一个此点的邻域,使函数在这个邻域有定义。我们又说函数在所定义的区间上每一点连续,那么什么区间才能使区间内每一点,都有一小邻域,使这个小邻域落在函数定义域之内呢?只有开区间具有这种性质,因为闭区间的两个端点不存在一个包含端点的小邻域,使它落在闭区间上。如此按照连续函数的一般定义,函数的连续性对闭区间就关闭了大门。这就需要引入左、右连续的概念。当然,对于连续性就没有左、右连续并相等这一说。因此,左(右)极限值等于函数在该点的函数值才是左(右)连续。
函数在点连续的特点是:当自变量在点的附近变化很小时,函数值的变化也很小。从上面的定义可以看出,函数在点连续的充要条件是:
① 函数
在
点有定义
② 当
时,左、右极限
和
存在且相等
③ 左、右极限等于
在
点的函数值。
若以上三个条件至少有一个不成立,则称在
点间断。
事物发展有渐变和突变,函数值也如此,即除有连续变化外,还有间断情形。因此对应连续点出现间断点。研究间断点的重要性,在一定的场合下并不亚于对连续性的研究。对间断点的研究是对间断点进行分类,并寻找不同类中间断点的特性。间断点就是破坏连续性的点,即不连续点。对于非边界的连续点来说,要求满足条件“左、右极限存在,并且极限值等于在该点的函数值”。如果破坏这些条件的任意一条,那么该点就是间断点。因为连续函数有比较“良好”的特性,所以间断点是按它与连续的“接近程度”来分类的。如此,间断点可以分为两大类。第一类间断点就是左、右极限都存在的间断点;第二类间断点,就是左极限或右极限至少有一个不存在的间断点。
3. 连续思想的内涵
古人云:“授人以鱼不如授人以渔”。“能点石成金的手指要比金山重要”。对数学的学习要注重于方法,方可起到以点带面的效果。数学思想方法是是数学思维的工具,是形成数学能力的必要条件。学生对数学思想方法的领悟和应用,必须通过教师的提炼、总结、点拨和培养才能形成。教师要充分利用这些材料,引导学生领悟、明晰数学思想方法,帮助学生学会“数学思考”,否则,就会失去数学思想方法训练的宝贵机会。
客观世界的许多现象和事物不仅是运动变化的,而且其运动变化的过程往往是连绵不断的,这些连绵不断发展变化的事物在量的方面的反映就是连续函数,连续函数就是刻画变量连续变化的数学模型。几何上,连续的直观含义就是连绵不断的,所以一个函数在上是一个“连续函数”的直观意义就是它的图象是一条连绵不断的曲线。从运动和变化观点来说,就是当逐渐改变时,函数的相应变动也是逐渐的,不会有任何突增或突减的跳跃式振荡。从数量上来说,逐渐的改变也就是逐步作微小的改变,所以当我们把函数的连续性局部化到的邻域来看时,在点连续的直观意义就是当在点的邻域内作微小变动时,相应函数值也在的自身的邻域内作微小变动。
3.1. 普遍联系的思想
数学证明中的分析法,就是从未知出发,寻求已知与未知的联系,最后化未知为已知的一种科学方法。众所周知,一个数学定理证明的最后书写形式,通常是一步一步“因为”、“所以”地从已知推到未知,由前提演绛出结论。但是,这个推导步骤的形成,一般说来,并不是一帆风顺的,因为有时已知的公式或定理浩如烟海,难以断定应从哪个已知条件出发,于是人们就常常把已知到未知的顺序颠倒过来,即从未知出发,通过联系的途径,揉索由已知通向未知的道路,从而形成所谓“执果索因”的分析法。正是连续的思想给我们了“执果索因”的力量。
3.2. 对立统一的思想
连续和间断是高等数学中通过极限方法分析的一个重要的数学内容,同时是一个古老而又极其重要的哲学范畴。人类对连续和间断问题的探讨,有着悠久的历史。它贯穿在科学和哲学发展的整个历史过程之中。所谓连续,是指物质结构及其发展过程在时间和空间上的毗邻性和持续性。所谓间断,是指物质结构及其发展过程在时间和空间上的分离性和跳跃性。事物和过程的连续和间断是对立的统一。它们相互包容、相互依存,彼此都不能单独存在。连续离不开间断,间断也离不开连续;连续中有间断,间断中也有连续,彼此都包含于对方。宇宙间的一切事物和过程无论处于何种状态都是连续和间断的辩证统一。随着现代数学的深入发展,对数量关系的连续和间断的辩证统一的认识更加深刻。比如:可数的线性有理数集,其自身是不连续的,但在极限处理条件下,它可以转化为连续的。有的连续量可通过离散值来确定,而认识离散数量的性质,也可以用连续量研究。函数的连续性和间断性是一个重要的知识点。但它的定义较抽象,学生不容易理解,也不容易记住。在介绍函数的连续性的时候,教师往往需要举出一些离散的间断值的变化趋势来说明函数的连续性。在分析函数的间断性的时候,如果单纯从高职高等数学内容的难度考虑,函数的间断点往往是有限个,除此之外其他点全是连续点。这种情况反映出函数是由连续点和间断点共同构成的,二者是对立的两种状态,但彼此之间又相互依存、相互包容。数学是关于现实世界空间形式和数量关系的科学,而现实世界又是充满着矛盾的统一整体,所以,作为现实世界一个侧面反映的数学,也必然是一个有着内在联系的有机整体。
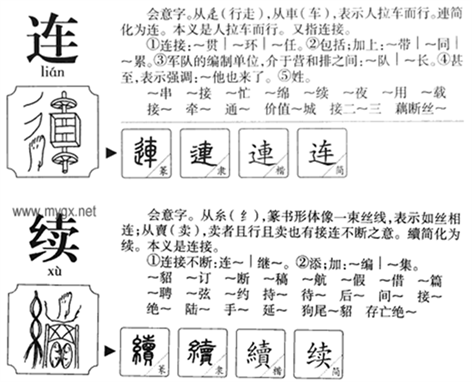
. oracle bone inscriptions of the characters “ligature” and “continue”
图3. “连”字和“续”字的甲骨文
4. 函数连续课程思政点
连续和间断不但是数学研究的对象,也是一对重要的哲学范畴。从数学的角度看,函数一般是连续和间断的统一体,从哲学的视角看,世界是连续性和非连续性的统一。自然界和社会领域的表现状态都是连续性和非连续性的统一,从自然、社会等角度探究连续性与非连续性的统一的普遍性及其与哲学基本原理的关系对于提升莘莘学子的学习之后的获得价值具有重要的促进作用,同时可以起到立德树人的效果。
4.1. 说文解字谈“连”“续”
中国选择中国特色社会主义制度,是由中国5000多年的历史文化决定的。中国特色社会主义制度是对中华优秀传统文化创造性转化与创新性发展的结果,具有一脉相承的历史性及独特的民族性。这说明,任何一个国家的制度和治理体系皆非凭空出现,一定有其历史文化的渊源。要理解函数的连续性,可以先从读懂中华优秀传统文化,特别是其典型代表“汉字”的文化基因开始(图3)。注重汉字研究,大力弘扬中华优秀传统文化,是实现用中国话语讲好中国故事、读懂中国制度的前提。然而,在数学课程中进行中华优秀传统文化的熏陶并不容易,但如果能够结合数学概念渗透一些中国优秀传统文化,比起直观的输入要自然一些,细腻一些。而且现在很多国人连古籍经典中的汉字都不认得、不理解,又如何深入经典,理解其中深邃的义理呢?
continuity [,kɔnti'nju:iti] = 词根词缀:continue 连续 -ity,而continue = con- 共同 -tin- 握,持有 ue. 连续性;to be uninterrupted;连续性就不是静态的,那是一种动态性的变化过程。这种动态的发展过程,是由量变积累引起部分的质变,在新的基础上再由新的量变积累引起新的部分质变的过程。实际上,纵览我们党对“社会主义初级阶段”的描述,都突出了社会主义初级阶段历史发展的过程性特征。可以说,社会主义初级阶段就是逐步摆脱不发达状态,逐步缩小同世界先进水平的差距,到基本实现社会主义现代化的历史阶段。
4.2. 可持续发展理念
可持续发展观强调人与自然关系的至上性,其核心是全球生态整体观。坚持绿水青山就是金山银山理念,坚持尊重自然、顺应自然、保护自然,坚持节约优先、保护优先、自然恢复为主,守住自然生态安全边界。深入实施可持续发展战略,完善生态文明领域统筹协调机制,构建生态文明体系,促进经济社会发展全面绿色转型,建设人与自然和谐共生的现代化。纵观历史和横贯东西,越是想去的长足的发展,也就是可持续的发展,也就越需要连续思维和战略思维。要顺应时代发展的变化,作出准确的判断和抉择,实现国家、民族和社会的可持续的发展。
4.3. 发展规划的连续性
习近平总书记在“中共中央关于制定国民经济和社会发展的十四五规划和2035远景目标的建议”中指出,要全力做好“十三五”规划收官和“十四五”规划编制工作;要乘势而上、奋力前行,推动“两个一百年”奋斗目标有机衔接,为全面建设社会主义现代化国家开好局、起好步。毋容置疑,展望未来,从历史发展的角度看,不论是十三五规划还是十四五规划以及2035远景目标都是实现民族复兴的中国梦的一段,是新时代中国特色社会主义道路中的一段历史场景,社会主义道路是连续的和可持续的。实现好、发展好就需要每一个历史的节点实现前一个规划和后一个规划的有效、有机、无裂痕和衔接。
中国共产党把马克思主义基本原理与中国具体实际相结合,不断推进马克思主义中国化,系统提出了社会主义初级阶段理论。社会主义初级阶段是一个动态发展过程,是逐步摆脱不发达状态,逐步缩小同世界先进水平的差距,直到基本实现现代化的历史阶段。全面建设社会主义现代化国家、基本实现社会主义现代化,是我国社会主义从初级阶段向更高阶段迈进的要求。习近平总书记在省部级主要领导干部学习贯彻党的十九届五中全会精神专题研讨班开班式上指出:“全面建设社会主义现代化国家、基本实现社会主义现代化,既是社会主义初级阶段我国发展的要求,也是我国社会主义从初级阶段向更高阶段迈进的要求。”我们应认真领会、充分把握这一新论断的深刻内涵和实践要求,在我国进入新发展阶段后,既立足现实,又着眼长远,为推动我国社会主义从初级阶段向更高阶段迈进而努力奋斗。
4.4. 五千年未曾间断的中华文明是函数连续性的体现
在几千年的历史演进中,中华民族创造了独特的中华文明,形成了关于国家制度和国家治理的丰富思想,包括大道之行、天下为公的大同理想,六合同风、四海一家的大一统传统,德主刑辅、以德化人的德治主张,民贵君轻、政在养民的民本思想,等贵贱均贫富、损有余补不足的平等观念,法不阿贵、绳不挠曲的正义追求,孝悌忠信、礼义廉耻的道德操守,任人唯贤、选贤与能的用人标准,周虽旧邦、其命维新的改革精神,亲仁善邻、协和万邦的外交之道,以和为贵、好战必亡的和平理念,等等。如今,纵观历史我们不难发现,从古至今除了我们中华文明之外,全球其实还诞生过不少的文明,比如说印度文明、埃及文明、罗马文明等等。只可惜随着时间的推移,这些文明也基本上都消失在了历史的长河之中,很多文明的成果,甚至是一个种族,更是早都灭绝了。笔者尽管不是文字研究学者,但从古文发表的文献和出版的论著中,可以看出“汉字”在中华文明的连续性中发挥的巨大作用,可以说它代表了民族的文化基因和堂堂做人的精神一直传承至今,是每一个华夏儿女的精神支柱。究其因是因为汉字的变化和发展是连续的,渐进的。再比如我们要实现探月计划,从最开始的规划到最近“嫦娥五号”带回月壤,也是一个连续的发展和持续的发力过程,其中体现的航天精神更是体现了民族的伟大梦想和伟大实践的有机结合(图4)。
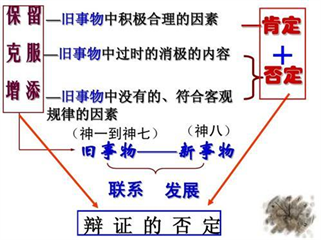
. dialectical relations in the continuum
图4. 连续中的辩证关系
5. 小结
本文以函数的连续概念为例,介绍如何将函数连续知识点与大学生的思想政治教育想结合,与中华文明的源远流长、国家的规划、党的治国理政的方针政策相结合。希望能够起到抛砖引玉的作用。
基金项目
2020年上海高校市级重点课程,2021年上海高校市级重点课程。上海理工大学市级课程思政培育课程项目《运筹学》《系统工程导论》。