1. 引言
1.1. 研究背景及意义
面对贸易战、芯片制约等技术挑战,我国的高新技术产业发展应得到全面的支持和发展。高新技术产业的发展不仅是某些地区,还要以长三角及珠三角为导向,带动其余地区共同发展高精尖技术,达到科技强国的目的。2020年10月,党的十九届五中全会强调“坚持创新在我国现代化建设全局中的核心地位,把科技自立自强作为国家发展的战略支撑”,着力解决“卡脖子”的技术问题。十四五时期将是我国实现产业升级与经济向高质量发展的关键转型期。因此,对高新技术产业竞争力的研究不仅关系到我国社会、经济的快速发展,更决定着我国在未来全球格局中的命运。
1.2. 研究思路及方法
本文以高新技术产业竞争能力为研究对象选取了我国31省市地区的九项指标作为高新技术产业竞争能力评价指标。文章构建了各地区高新技术产业发展的内部竞争力、外部竞争力两个一级指标,内部竞争力下包含了科创投入力度及科创产出能力两个二级指标及r & d (研究与试验发展)人员折合当时全量、r & d经费、专利申请数、专利授权数、新产品消费收入五个三级指标;外部竞争力下包含了科创环境一个二级指标及高等学历平均在校人数、科技研究从业人员、r & d项目数、技术市场成交额四个三级指标。文章先利用了k-means聚类分析法将各地区聚为了先导、发达、一般、落后4个类别;由于高新技术产业的竞争能力的指标体系较为复杂,且这些指标间存在一定的相关性而造成数据冗余,故采用因子分析法提取两个主要的公共因子,并计算各地区相应的得分,最后针对模型结果给出针对性建议。
1.3. 文献综述
在构建高新技术产业竞争能力评价体系中,潘霞等(2013)从内在竞争和外在竞争两个方面划分九个影响因素 [1] 进行分析,肖娟(2015)对中部地区高新技术产业竞争力进行了静态和动态相结合 [2] 的评价分析,陈红川(2017)以政策、市场、人才为三个一级指标并下设八个二级指标 [3],建立评价体系;周燕(2018)根据国内外学者对科技竞争力方面的研究从区域科研机构科技创新水平、高技术产业科技创新水平、区域工业企业科技创新水平以及区域教育水平 [4] 4个方面选取了25个指标。王洪庆(2017)从行业角度构建了不同行业的高新技术创新能力评价体系,并运用熵值法探究了18个高新技术行业发展及创新能力的差异 [5]。
在实证研究高新技术产业发展及竞争能力评价方面,王洪庆(2017)运用熵值法 [5] 对18个高新技术行业的技术创新能力进行比较分析。何平(2018)结合高技术产业技术创新的特点,构建了高技术产业技术创新能力的“弓–弦–箭”模型 [6] 并构建了基于熵值和数据包络分析(dea)法的高技术产业技术创新能力评价模型。钮亮等(2019)将局部moran指数和k-means聚类方法结合在一起实现了多变量空间聚类,将高新技术产业聚为了热点区域及冷点区域 [7]。
2. 模型构建及评价指标的确定
2.1. 数据来源
样本数据来自中国统计年鉴2020年我国高新技术产业发展数据。数据包含9个变量分别为:每十万人口中高等学校平均在校人数(x1)、科学研究和技术从业人员(x2)、r & d人员折合全时当(x3)、r & d经费(x4)、r & d项目数(x5)、技术市场成交额(x6)、专利申请数(x7)、专利授权数(x8)、新产品消费收入(x9)。数据包含31个“观测值”,分别对应中国31个省、市、自治区的高新技术发展。
2.2. 评价指标
笔者在知网查阅了大量关于高新技术产业发展的现状、结构、竞争评价体系等方面的文献,参考肖宇琛(2019)、彭隆美(2019)、潘霞(2013)等人的文献,确立了评估我国高新技术产业发展竞争能力评价体系指标,评价指标如表1所示。
. competition evaluation indicators
表1. 竞争评价指标
2.3. 模型构建
2.3.1. k-means聚类分析模型
在层次聚类中,一旦个体被分入一个族群,它将不可再被归入另一个族群,而k-means聚类能弥补层次聚类的不足,它的建模思想为:在所有要聚类的对象中,任意选择k个对象作为初始聚类中心,计算每个对象与聚类中心的距离,并根据最小距离重新划分,循环计算聚类中心至聚类中心不再改变。
2.3.2. 因子分析模型构建
因子分析的目的是用少数几个综合因子去描述许多具有复杂关系变量的一种多变量统计分析方法,也是利用降维的思想。其基本思想是将相关比较紧密的几个变量分在同一类,相关性较低的变量归在不同类,每一类变量就是一个公共因子。前面的k-means聚类法仅把我国各地区高新技术发展分为四类,存在一定的缺陷,因此利用因子分析找出几个真正影响高新技术发展的公共因子。
因子分析法是从变量内部相关度出发。根据变量的相关度进行分组并提取公共因子。将每个因子对总体的方差贡献率作为权重,将各因子乘以权重相加得到因子得分。因子分析模型如下:
(1)
其中aim表示因子载荷,ei表示特殊因子。
第i个公共因子得分函数表示为:
(2)
其中cij表示标准化后公共因子得分矩阵中的元素,di表示标准化后的指标数值。
3. 实证分析
3.1. 数据预处理
为了消除原来各指标量纲,使各指标之间具有可比性,需要对原始数据进行标准化处理。经过处理后的数据的相关系数矩阵由r表示,其中rjk表示第j和第k个变量之间的样本相关系数。
,经过处理后的数据的相关系数矩阵由r表示,其中
,表示第j和第k个变量之间的样本相关系数。
3.2. k-means聚类分析模型
k-means聚类碎石图如图1所示。根据碎石图显示,应当将31省市分为4类,聚类1、2、3、4分别代表高新技术超发达、高新技术发达、高新技术较发达、高新技术落后。具体聚类结果如表2所示。2020年我国高新技术产业发展k-means聚类分析结果表明:广东、江苏、浙江聚为第一类地区即高新技术超发达地区,这类地区经济发达属于一线城市,城镇居民收入高,各项政策获得的经费及拨款多,教育发展也发达,进而高新技术产业也很发达,聚类结果符合实际情况;北京聚为第二类地区即高新技术发达地区,但由于北京的高新技术发展结构存在不平衡情况,故归为第二类发达地区;天津、河北、辽宁、上海、安徽、福建、江西、山东、河南、湖北、湖南、重庆、四川、陕西聚为第三类即高新技术较发达地区,但从图2聚类结果散点图看出,这类组别内的样本差异较大,较为分散,如辽宁虽被聚到了较发达地区,但与同组的上海、山东等地区的差距较大。其余山西、黑龙江、吉林、青海、西藏等13个省份聚为第四类地区高新技术发展落后地区,同组内的差距相对比较小。
2020年我国高新技术产业发展k-means聚类分析结果表明:广东、江苏、浙江聚为第一类地区即高新技术超发达地区,这类地区经济发达属于一线城市,城镇居民收入高,各项政策获得的经费及拨款多,教育发展也发达,进而高新技术产业也很发达,聚类结果符合实际情况;北京聚为第二类地区即高新技术发达地区,但由于北京的高新技术发展结构存在不平衡情况,故归为第二类发达地区;天津、河北、辽宁、上海、安徽、福建、江西、山东、河南、湖北、湖南、重庆、四川、陕西聚为第三类即高新技术发展一般地区,但从图2聚类结果散点图看出,这类组别内的样本差异较大,较为分散,如辽宁虽被聚到了发展一般类别中,但与同组的上海、山东等地区的差距较大。其余山西、黑龙江、吉林、青海、西藏等13个省份聚为第四类地区高新技术发展落后地区,同组内的差距相对比较小。k-means聚类虽然存在一定缺陷,但总体聚类效果对比于层次聚类较好。
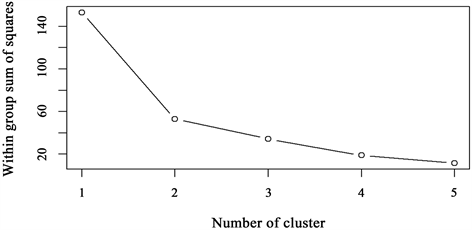
. gravel diagram
图1. 碎石图
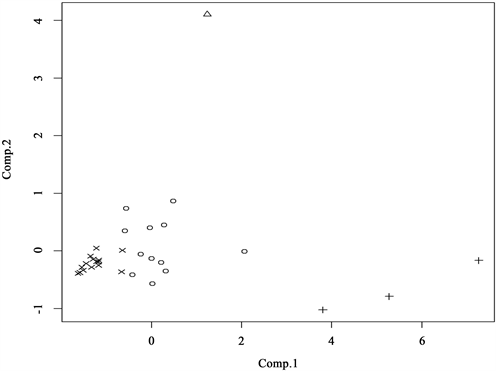
. k-means clustering result scatter distribution plot
图2. k-means聚类结果散点分布图
. clustering results in 31 provinces and cities
表2. 31省市聚类结果
3.3. 因子分析
3.3.1. 初始因子分析
取2个因子对样本数据进行采用主成份法进行因子分析,结果如表3所示。表3中,第一个因子(f1)解释原有9个变量总方差的75%,累计方差贡献率为75%。第二个因子(f2)解释原有8个变量总方差的19%,累计方差贡献率为94%。由于当公共因子数为2时,累计方差贡献率达94%,包含了原始数据的绝大部分信息,因此选取两个公共因子作为评价各地区高新技术发展的竞争因子。
. initial factor analysis results
表3. 初始因子分析结果
3.3.2. 旋转载荷
为了使得各因子的值差别更大以便于解释各因子含义,对样本数据进行因子正交旋转并计算因子得分,正交旋转之后的载荷矩阵如表4所示。从结果可以看出,第一个公共因子f1在r & d人员折合全时当量(x3)、r & d经费(x4)、r & d项目数(x5)、专利申请数(x7)、专利授权数(x8)以及新产品消费收入(x9)上的载荷值均具有较高的载荷,且载荷接近于1,说明第1个因子(f1)主要解释了这六个变量的特征,命名为“高新技术产出能力”因子。第二个公共因子f2在x1 (每十万人口中高等学校平均在校人数)、x2 (科学研究和技术从业人员)、x6 (技术市场交易额)变量上的载荷值较大且接近于1,由此说明第2个因子(f2)主要解释了这三个变量的特征,可命名为“高新技术环境支持”因子。
3.3.3. 因子得分
若要得出各省市地区高新技术发展结构和能力的优势与不足,需要计算各省市地区在“高新技术产出能力”因子(f1)、“高新技术环境支持”因子(f2)这2个因子及综合发展及结构水平能力方面的得分,以此作为评价依据。因子得分模型为:
。
以各因子的方差贡献率占两个因子总方差贡献率的比重作为权重进行加权汇总,算出各地区的综合得分f,
,公共因子及综合得分如表5所示。
. rotate the load matrix
表4. 旋转载荷矩阵
. 31 provinces and cities factor score table
表5. 31省市因子得分表
第一个竞争因子f1 (高新技术产出能力)得分前五名地是广东、江苏、浙江、山东、北京,其中广东的得分为3.47,江苏得分为2.52,浙江得分为1.73,这些地区得分均超过1,远远高于其他地区,说明广东、江苏、浙江,三地经济发达,人均收入高,得到的科研经费高,因而科技创新能力产出结果也远远高于其他地区,与实际情况比较接近。f1得分后五个地区分别是西藏、青海、海南、宁夏、新疆。这些地区是少数民族聚集地,经济发展以畜牧业、农业为主,经济发展相对落后,教育相对也不发达,因而高新技术发展也落后。
第二个竞争因子f2 (高新技术环境支持)得分前五名的地区分别是北京、陕西、天津、上海、湖北,除湖北外的四地区f2得分均大于1。一方面这些地区均为一线或新一线城市,经济发展状况好吸引大量优秀毕业生进入这些城市工作;另一方面这些地区的高校数量也非常多为高新技术的发展提供了潜在发展能力。而得分最后五名的地区分别是浙江、青海、江苏、西藏、广东。青海及西藏的经济发展相对落后,这些地区的高校数量相对较少,高校在校人数较少,潜在科技创新竞争力较低;而浙江、江苏、广东三地虽然在f1因子上得分较高,但在f2因子上得分较低,说明这些地区高新技术发展较迅猛但发展结构存在不平衡问题。
综合得分f较高的主要是长三角、珠三角地区及东部地区的一些发达省份,而中西部及少数民族聚集地的得分较低,高新技术发展落后,高新技术产出能力低下,高新技术环境支持也不到位。总体来看,高新技术发展状况呈现空间性差异及区域性不均衡。
4. 结论与建议
4.1. 加大对中西部扶持力度
高新技术发展现状呈区域性不均衡,位于中西部及少数民族地区的省份由于经济不发达、地理位置受限、政府支持力度弱等原因导致高新技术发展受限。政府应加大对中西部高新技术发展的支持力度,加大高新技术资金投入;建立健全的人才引进政策,吸引高校毕业生到中西部及少数民族地区从事科技创新工作,扩大并优化科创队伍;改善高新技术发展潜在环境,缩小与东部发达地区的差异。
4.2. 建立对点帮扶机制
以广东为核心的珠江三角洲,以江苏、浙江为核心的长江三角洲以及北京,作为高新技术发展的先导、旗帜性区域被视为其他地区发展的标杆。可以采用区域帮扶模式,以这些地方为中心,向邻近的技术落后地区支援,建立对点帮扶机制。定期派发达区域科创人员到中西部及少数民族地区进行指导,并加强合作交流;同时向落后地区提供到现场的学习观摩机会,进一步缩小地区差异性。另外,落后区域之间也可以开展联合工作,互惠公补。
4.3. 加大r & d经费投入
高新技术产业的发展和创新离不开r & d经费的支持,长三角及珠三角地区经济基础发达,政府对科研及技术创新的资金拨款也较高,故这些地区的高新技术产业发展十分迅猛。因此,需要加大r & d经费投入,同时尽力降低研发成本,提高科研创新力及科研成功率。同时,学习引进国外先进设备系统、研发体系,用充足的资金提高科技转化率并加快高新技术转化为生产力的速度。
4.4. 加大产学联合力度
本文构建的高新技术产业竞争能力评价体系中的外部竞争力包含高等学校平均在校人数及科技研究从业人员,这两项指标对高新技术产业的发展起到了主导性作用。高新技术的发展不仅需要科研院所、政府等主体的参与,还需要高校、企业、金融机构等主体参与。科研院所向高校提供实习地、训练基地,高校向科研院所提供科创人员并为新技术的开发提供思路和帮助,改善高新技术发展的环境;企业及金融机构等向科研院所提供资金支持,让资本市场为高新技术发展提供活力,科研院所为企业和金融机构提供凯发国际一触即发的技术支持。社会多方主体达到互惠互利、合作共赢的结果,促进高新技术的发展,集中力量发展我国“卡脖子”的技术问题,尤其在芯片设计、航空航天、电子元件、医药医学、电子通信等方面的技术开发和创新。