1. 引言
在高等数学中,泰勒中值定理及对应的泰勒公式是课程的重点内容,也是难点,在微积分学中应用广泛。泰勒公式是以英国著名数学家泰勒(taylor, 1685~1731)命名的。泰勒是早期牛顿学派最优秀的代表人物之一,也是有限差分理论的奠基人 [1] 。泰勒的重要著作有《正的和反的增量方法》和《线性透视论》等。早在1712年泰勒就得到了现代形式的泰勒公式。泰勒公式的思想是用简单的多项式函数来近似代替复杂函数。多项式函数具有很多优良的性质,比如容易用数值软件计算其函数值,其导数与积分仍为多项式等。
泰勒公式及其应用在微积分学中占有非常重要的地位。泰勒公式的实质是用函数在某点的函数值及导数值描述其附近邻域内的性质,核心思想是应用“逼近法”求函数的值。在高等数学中,可以应用泰勒公式证明不等式、中值问题、近似计算、极限计算、判断级数与广义积分的敛散性等方面。本文通过对泰勒中值定理思想方法的解读,分析比较两个泰勒中值定理的条件、结论和适用情形,然后探讨泰勒公式的拓展应用。本文着重讨论利用泰勒中值定理证明曲线的凹凸性判定定理,证明某些中值问题,近似计算,以及利用幂级数求解微分方程等应用。
2. 泰勒中值定理及思想方法
微分的思想本质上是“以直代曲”,即在某点的邻域内用切线近似曲线的思想。具体而言,设函数
在某区间内有定义,点
及
在该区间内,如果函数的增量可以表示为
,其中a是不依赖于
的常数,则称函数在点
是可微的,并且这时
。由此,我们可以得到函数的一阶近似,即在
的小邻域内有如下近似:
这种近似表达式的近似程度不高,其误差是关于x的高价无穷小。为了提高近似的精确度,我们考虑用更高次的多项式来近似函数。即寻找一个n次多项式
,使得两个函数
和
在
处的函数值及直到n阶导数值均相等,即
,且
经过简单的计算,可得如下的n次多项式
的表达式
(1.1)
该多项式又称为泰勒多项式。多项式
和
的误差称为n阶余项,记为
。
下面我们以正弦函数为例,用不同次数的泰勒多项式近似函数。取
,则函数在
的小邻域内的一阶近似为
。经过计算可得,
对应于公式(1.1)的泰勒多项式为
如果m分别取
,比较泰勒多项式与正弦函数的图形,随着多项式次数的增加,多项式对函数的近似程度越来越高,误差越来越小,具体可见图1和图2。特别地,当m取6时,对应的11次泰勒多项式与正弦函数的图形在区间
上非常接近。由此可见,用泰勒多项式来近似表达函数是非常合理的。
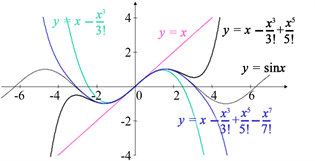
. the graph of sine function and its taylor polynomial of degree n, n = 1, 3, 5, 7
图1. 正弦函数及其n次泰勒多项式的图形,n = 1,3,5,7

. the graph of sine function and its taylor polynomial of degree n, n = 9, 11
图2. 正弦函数及其n次泰勒多项式的图形,n = 9,11
对于余项的估计,当
时,我们由微分的定义可知
。将这个思想推广一下,即证得下面的第一个泰勒中值定理 [2] 。
泰勒中值定理1如果函数
在点
处具有n阶导数,则存在
的一个邻域,对该邻域内的任一x,有
,其中
。
定理的证明用到洛必达法则,高价无穷小的定义,以及n阶导数的定义。该定理中的余项称为佩亚诺(peano)余项。如果取
,得到带有佩亚诺余项的麦克劳林(maclaurin)公式
大多数通用的教材中,都会给出几个常用函数的麦克劳林公式,包括指数函数
,三角函数
,幂函数
和对数函数
等。与这几类函数有关的复杂的极限题目,可以利用带有佩亚诺余项的麦克劳林公式求解。例如,正弦函数
带有佩亚诺余项的麦克劳林公式为
佩亚诺余项可以用于求解某些极限,但是不能具体估算误差的大小,为此我们给出第二个泰勒中值定理 [2] 。
泰勒中值定理2如果函数
在
的某个邻域
内具有
阶导数,则对任一
,有
,其中
,这里
是介于x与
之间的某个值。
该定理的证明主要用到柯西中值定理,定理中的余项称为拉格朗日(lagrange)余项。特别地,当
时,泰勒公式变成拉格朗日中值公式
这里
是介于x与
之间,因此,泰勒中值定理2是拉格朗日中值的推广。当
时,泰勒公式变成
(1.2)
比较两个泰勒中值定理,第二个定理的条件要求高,结论也更精确。在进行误差估计或者证明一些中值问题时,经常用到带有拉格朗日余项的泰勒公式。
3. 凹凸性的判定定理
函数的单调性反映在图形上,就是曲线的上升或下降。但是,在曲线的升降过程中,还有曲线弯曲方向的问题,即凹凸性的判定。如果函数具有二阶导数,那么可以用二阶导数的符号判断曲线的凹凸性,有下述定理 [2] 。
定理3.1设函数
在
上连续,在
内具有一阶和二阶导数,则
1) 如果在
内
,则
在
上的图形是凹的;
2) 如果在
内
,则
在
上的图形是凸的。
分析:在很多教材中,利用拉格朗日中值公式证明该判定定理,但是思路比较复杂,需要连续两次应用中值公式,不太容易掌握。事实上,可以直接应用泰勒中值定理2证明该定理,证明过程清晰明了。
证明对情形(1),设
和
为
内任意两点,不妨设
。记
,则
在
处的泰勒中值公式为
分别将
和
代入上式,得
因为
,且
,故上述两式相加,得
。
即证得
,由定义,函数
在
上的图形是凹的。类似地可证明情形(2)。
4. 拓展应用
4.1. 近似计算
有了函数的泰勒展开式之后,可以用它进行近似计算,计算的精度由拉格朗日余项进行估计。
例4.1估计无理数e的值,要求误差不超过10−6。
解函数
的麦克劳林公式为
。
这时,近似的误差为
。
取
,得到无理数e的近似式为
其误差为
当n = 10时,计算得
,其误差不超过10−6。
例4.2估计无理数
的值,要求误差不超过0.001。
解因为函数
具有任意阶导数,其泰勒级数为
令
,得
。
其余项为
取n = 4,可得
此时误差符合要求,故取n = 4,计算时取四位小数可得
。
4.2. 证明中值问题
例4.3函数
在
上二阶可导,
,
。证明:
,
。
证明
在
上二阶可导,由泰勒中值定理2,将
在x处展开,得
,
,
所以
。由已知条件,
,
,故
,
进一步,
。
记函数
,开口向上的抛物线,故其最大值在区间端点处取得。又因
,
,所以
。故
,
即证得
。
下述例题为2023年全国硕士研究生入学统一考试数学一试卷的第20题,综合应用了泰勒公式,微积分学中的费马引理,以及连续函数的介值定理等。
例4.4设函数
在
上具有2阶连续导数,证明:
1) 若
,则存在
,使得
;
2) 若
在
内取得极值,则存在
,使得
。
证明因为
,故
在
处的泰勒公式为
,
其中c介于0与x之间。将区间两端点
分别代入上式,得
, (4.1)
, (4.2)
由(4.1)和(4.2)两式相加,得
,
即
。
因为
在
上具有2阶连续导数,所以
在
上存在最大值m与最小值m,这时,
。根据闭区间上连续函数的介值定理可得,存在
,使得
,即
成立;
3) 若
在
内取得极值,不妨设
为其极值点,则由费马引理可得,
。将
在
处泰勒展开,
,
其中d介于
与x之间。带入两个端点,
,
。
两式相减可得:
。
所以
,
记
,则
。
因为
,所以
成立,结论得证。
分析上面两个例题,泰勒中值定理在证明中值问题时,解题方法非常灵活。我们在分析题目时,需要选取合适点处的泰勒展开式,一般选取区间端点,区间中点,或者区间内任一点x处的泰勒公式,然后充分利用已知条件证明结论。
由拉格朗日中值定理,设
在点x处的增量为
,则相应的函数增量为
,其中
,
该公式也称为有限增量公式。方便起见,记
。关于公式中的
,我们进一步得到下列命题。
命题4.1.设
二阶可导,且
,则由有限增量公式,存在
,使得
。证明:
。
证明由有限增量公式,
,其中
。 (4.3)
另一方面,因为
二阶可导,则由x处的泰勒公式,得
。 (4.4)
(4.3)和(4.4)两式相减,得
。
上述等式同除
,得
。 (4.5)
令
得,
。
进一步,由(4.5)式得,
。即证得
。
上述命题可以推广到更高阶导数。
命题4.2.设
在
有
阶导数,且
,由泰勒中值定理,存在
,使得
。证明:
。
证明由泰勒中值定理2,
在
处带有拉格朗日余项的泰勒展开式为
,
另一方面,带有佩亚诺余项的泰勒展开式为
两者相减,得
两边同除
,再同乘
,得
又因
,上式两边令
得,
。
4.3. 微分方程的幂级数解
如果函数
在
的某个邻域
内具有任意阶导数,则
在该邻域内的泰勒公式可以写为函数项级数
由泰勒中值定理,可以得到下述定理。
定理4.3设函数
在
的某个邻域
内具有各阶导数,则
在该邻域内能展开成泰勒级数的充分必要条件是泰勒公式中的余项
当
时的极限为零。
前述我们主要讨论一元函数的泰勒公式和泰勒级数,多元函数也有相应的泰勒级数。泰勒级数属于幂级数,在微积分学中应用广泛。比如求解常微分方程时,为了扩大微分方程的求解范围,需要用级数解法求解某些微分方程。法国数学家柯西(cauchy)是第一个从理论上研究初值问题幂级数解的数学家。考虑如下的微分方程初值问题;
。 (4.6)
这里函数
在区域
内解析,即对于g内任一点
,
在
的某个邻域内可展开为收敛的泰勒级数
。
柯西用优级数法证明了如下的存在唯一性定理 [3] 。
定理4.4 (柯西定理)如果函数
在矩形区域
内可展开成
和
的一个收敛的泰勒级数(幂级数),则初值问题(4.6)在
点的某个邻域内有一个解析解,而且它是唯一的。
例4.5 用幂级数解法求解airy方程
在
处展开的幂级数解。为此,把方程改写成
,设其幂级数解的形式为
,进而有
。代入方程,再利用幂级数展式的唯一性得到系数的递推公式,最后得到所求的幂级数解为
例4.6 用幂级数解法求解微分方程
。
解设
是方程的解,代入方程,得
将上式左边第一个级数写成
,则有
。
比较系数,得
即
,
或写成
于是方程的幂级数解为
。
除此之外,可以用幂级数解法求解勒让德方程和用广义幂级数解法求解贝塞尔方程等。
5. 结语
本文主要探讨了泰勒中值定理的思想方法,利用泰勒公式证明了曲线凹凸性的判定定理,讨论了拉格朗日余项中
的极限性质,以及泰勒级数在微分方程求解中的应用。事实上,泰勒中值定理及泰勒级数在微积分学中具有非常重要和广泛的应用 [4] ,如近似计算,研究函数的性质等。利用幂级数不仅可以计算某些函数的近似值,还可以计算一些定积分的近似值。此外,泰勒公式在很多工程技术问题中也有重要应用 [5] ,比如利用泰勒公式可以推导出光学测量技术中变形函数的位移等。