1. 引言
综合与实践课是《义务教育课程方案(2022年版)》中明确规定要开展的课程,与劳动一起每周开展不少于一课时 [1] 。在《义务教育数学课程标准(2022年版)》(以下简称“新课标”)中,综合与实践和数与代数、图形与几何、统计与概率并列为初中数学四大板块的课程内容,旨在培养符合学生长期发展需要的的核心素养:会用数学的眼光观察现实世界、会用数学的思维思考现实世界和会用数学的语言表达现实世界。在小学阶段,综合与实践主要以主题式学习为主,初中阶段则以项目式学习为主,到了高中则延伸发展为“数学建模活动与数学探究活动”,其本质都是真实情境下的问题解决。
综合与实践的雏形是2001年颁布的《全日制义务教育数学课程标准(实验稿)》中“实践与综合应用”。2011年,“综合与实践”在《义务教育数学课程标准(2011年版)》中正式被提出。2022年颁布的新课标继续将“综合与实践”的内容具体化,对小学和初中两个阶段分别做出不同的内容要求。在三代课标的指引下,综合与实践这一领域被越来越多的专家、学者以及一线教师关注和研究。
综合与实践的顶层设计方面的研究有童玉婷 [2] 、孙虎 [3] 、李海东 [4] 等学者,探究了综合与实践整体上的开展实施路径、内涵、价值、关键特征、教学评价等方面的内容。也有硕士研究生结合国内外较先进的教学学习理念或模式,开发了初中数学综合与实践课程 [5] [6] [7] 。此外还有的学者对综合与实践教学开展了现状调查 [8] [9] [10] ,针对教学现状开发综合与实践教学的策略。得益于建构主义学习理论在我国的不断推广,综合与实践教学的研究逐渐成为热点,并将持续发酵。
数学建模是连接数学与实际生活的重要方式。美国最早举办了大学生数学建模竞赛(mcm),而我国在1992年开始每年举办一届大学生数学建模竞赛。数学建模在大学教育中的发展最早,也最为成熟。随着数学在各学科领域的重要性日益凸显,数学建模也开始融入到中小学教育中,目前已经有学者进行了有关初中数学建模的研究 [11] [12] [13] 。将数学建模纳入综合与实践教学中,能够体现学生的主体性,激发学生学习的积极性,在问题解决中形成“三会”核心素养。
2. 数学建模融入综合与实践教学的可行性
2.1. 数学课程标准的宏观设计
新课标进一步强调了数学课程的性质。数学的研究对象源于对现实世界的抽象,对研究对象的模型构建等研究中形成了数学的结论与方法,帮助人类认识观察、思考和表达现实世界的本质、联系和规律。综合与实践作为中学数学课程内容中的四大板块之一,在课标中具有重要的地位。《义务教育数学课程标准(2011年版)》中阐明了中学数学课程设计的思路,要体现数学知识与技能的结果同时注重学生通过已有的经验去经历从现实背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程 [14] 。2022年颁布的新课标对初中数学综合与实践的学业要求学生通过与他人合作,提出解决现实情境当中问题的思路,分析问题,构建数学模型,通过合理使用数据借助模型得到结论等 [15] 。
2.2. 教育教学理论的相关支撑
数学建模是一类数学活动,也是一种项目式学习。项目式学习就是在教师的引导下,以真实的情景为基础,让学生自己去发现问题,分析问题,解决问题,并展示结果的一种学习方法。初中数学综合和实践主要是以项目式学习为主,在初中数学综合和实践教学中,项目式学习理论已进行了大量的实践研究,将数学建模融入到综合和实践教学中,已有相关研究的基础存在。著名教学心理学家皮亚杰主张活动教学法对发展学生的认知能力、学习兴趣、创造能力等方面都具有十分重要的作用。活动教学法是一种通过各类活动形式使学生主动参与学习、积极思考和创造的教学方法。它注重学生自主的参与求知的过程,通过亲自经历实践和动手操作的形式习得知识。不仅能加深学生对知识的理解和掌握,还能激发学生的发散性思维,培养学生的问题解决能力。像建构主义学习理论、弗赖登塔尔数学教育观等理论对本研究的支撑不再赘述,总之,诸多教育教学理论对数学建模融入综合与实践教学的开展具有重大的指导作用。
3. 数学建模融入综合与实践教学的必要性
3.1. 课程价值,凸显育人目标的需要
初中数学综合与实践的教学,不再是以数学学科知识的学习或运用为主,最要体现的是跨学科、跨领域之间的联动性,目的在于培养学生的能力和素养,促进学生的全面发展。数学建模活动,是运用数学知识、数学思想,建立数学模型解决生活实际当中存在的问题的活动,它虽然基于数学,但是与其他学科或领域的联系性特别强。参考历年的全国大学生数学建模竞赛题目就会发现,没有任何一个题目能单靠数学一个学科的知识解决,它可能会涉及物理、化学、生物、经济学、地理、医学等众多学科领域的知识,数学建模旨在培养学生信息检索分析能力、实操能力、创新意识等多方面能力素养。所以无论是综合与实践教学还是数学建模,它们对学生的培养目标是如出一辙的,结合数学建模活动开展数学综合与实践的教学,设计合理的教学活动,能够达到一加一大于二的教学效果。
3.2. 立足学科,突出课程特征的需要
数学建模活动与综合与实践教学都强调过程的实践性。数学建模要实现从理论到现实的跨越,最关键的一步是模型的应用。数学建模不仅要把综合复杂的现实问题通过定量、定性等分析转化为数学问题,建立数学模型,更重要的是模型检验阶段。通过检验模型的效果,不仅是评价数学建模整体效果的重要指标之一,也是培养参与者的将理论付诸于实践的能力的重要一环,通过对数学模型进行应用,有利于培养学生的应用意识,感受数学与广大生活生产的联系。数学建模活动中较强的实践操作性,能够激发学生对数学学习的兴趣,培养学生学习的主动性,提高学生的核心素养,这也是综合与实践教学所追求。
初中数学的综合与实践教学,应该融合多学科、多领域而开展,但也要立足于数学。而数学建模活动契合这一要点。以数学建模的形式开展综合与实践教学,不会使综合与实践教学变成普通的学科知识传授的课堂,同时可以兼顾在多学科多领域的融合过程中突出数学学习的重要地位。
3.3. 人才培养,服务社会创新发展的需要
当前社会对人才的需求日益提高,不再仅仅追求在某一特定专业领域的专精,更加强调人才在跨学科融合的环境中的综合能力。除了对某一领域的专业技能要求之外,社会工作也迫切需要人才能够整合信息、快速学习,并能够在复杂多样的现实问题中提供凯发国际一触即发的解决方案。举例而言,我国的科学家们成功将3d打印技术与医学领域相结合,显著改善了临床手术治疗的精准度,同时也降低了手术的风险。通过这种多学科的融合应用,不仅在技术上取得了显著的进步,更为社会提供了创新性的凯发国际一触即发的解决方案。此外,积极开展数学建模活动不仅仅是为了提升学生在数学方面的知识与技能,更为重要的是培养学生的综合素养,提高其在未来发展中的竞争力。因此,现代社会对人才的要求已经不再局限于单一领域,而是倡导跨学科融合,强调综合能力的培养。这种综合性的要求使得人才在面对多元化的挑战时能够更为从容地应对,为社会的进步和发展贡献更多可能性。
4. 数学建模融入综合与实践教学的应用示例
数学建模活动是通过在实际情境中进行数学抽象,运用数学语言表达问题,并借助数学方法建立模型来解决问题的过程。其基本过程(如图1所示)主要包括以下步骤:首先,在现实情境中从数学的角度发现问题然后提出问题;接着,通过对问题进行深入分析,建立相应的数学模型;随后,利用模型中的参数进行计算和求解,验证模型的可行性;同时,通过优化模型,进一步提高解决问题的效果;最终成功解决实际问题。
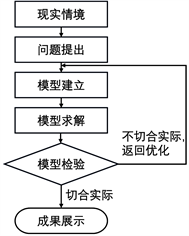
. the basic process of mathematical modeling activities
图1. 数学建模活动的基本过程
数学建模活动,是以数学思维为基础,在实际情境中,从数学角度抽象出相关问题,用数学语言描述问题,并利用所学知识进行分析、处理、解决实际问题的一类综合实践活动。数学建模方法使问题在数学框架下得到全面而深入的处理,为解决实际问题提供了有效的途径。通过这样的过程,学生经历了建立模型、分析与解释、应用与推广等环节,发展模型思想和应用意识等能力,形成学科核心素养。
开展数学建模活动,教师作为学生学习指导者角色的作用对学习效果的达成是十分关键的。首先教师要在课前确定好活动主题,设计好问题情境,做好预备,例如活动开展需要用到的物品,对整节课的活动流程有一个整体的把握。教学开始后首先要引导学生进入情境,一起发现问题并提出,然后指导学生经历模型建立、求解、检验等过程,模型的分析与检验又可以进行反馈,对模型建立进行优化,进一步得到更优解,最后得出解决方法并进行成果展示,成果展示可以以课题报告等形式。
下面以《鞋号问题》这一案例为例,具体分析如何将数学建模融入初中数学综合与实践教学中。本案例可作为八年级下册的综合与实践教学活动。《鞋号问题》一例源于新的高中数学课程标准后第26个案例,此案例所对应的教材知识内容是初中数学八年级下册第十九章——一次函数,有关鞋号问题的题目也时常出现在初中数学的练习中。从学情上分析,在学习完一次函数后,学生已具备知识经验。
4.1. 创设现实情境,发现问题
“千里之行,始于足下”。2022年6月5日,中国问天实验舱宇航员陈冬、刘洋和蔡旭哲担任中国航天员首次在轨进入科学实验舱任务执行者,成功发射升空。航天员们在太空中完成了装修“新家”、建立载人环境、开展在轨科学实验、休闲锻炼等系列任务和活动。航天员们所穿的舱内用鞋“出镜率”十分高,长达半年的“出差”时间里,舒适的鞋子尤为重要。如今网购已成为主流购物方式之一,在网购时如何选择一双合适自己的鞋子呢?
【设计意图】:以问题情境,展示我国航天事业取得的辉煌成绩,培养学生的民族自豪感,自信心,凝聚力。与此同时,初中生正处在青春期,他们的身体正在快速地成长,换鞋买鞋都是和他们密切相关的事物,能够激发他们的好奇,激发他们的学习兴趣,在现实生活中发现问题。
4.2. 基于数学抽象,提出问题
随着互联网的飞速发展,网购已经是每家每户重要的购物手段之一。网购和实体店购物对比有利也有弊。以购买鞋子为例,网购鞋子时不能像实体店一样通过多次试穿选择自己合适的鞋号。一般商家会给出部分脚长与鞋号的对应参数(见表1)。
. shoe size and foot length correspondence table
表1. 脚长和鞋号对应表
请解决以下问题:
问题一:在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你能发现脚长和鞋号的变化有什么规律吗?
问题二:鞋号y是否为脚长x的函数?如果是,试着构建出符合表中数据的函数解析式,并画出此函数的图像。此函数能够表示该表中脚长与鞋号的变化规律吗?
问题三:某运动员的脚长为272 mm,请问他该买多大号的鞋?动手量一量自己的脚长,根据你的脚长选择合适的鞋号。
【设计意图】:经过从现实情境中发现问题后,教师在情境的依托上给出具体的驱动问题。在问题的驱动下,使学生体会现实生活与数学的联系,培养学生用数学的眼光观察我们的现实世界。驱动问题的设计层层递进、环环相扣,学生能够由易到难,逐步思考、分析、建立模型解决问题。并且关注了教学的实践性,让学生动手测量自己的脚长,通过模型得出所穿鞋号,一方面检验了模型是否合乎实际,另一方面让学生在实践中进一步感受数学的生活化。
4.3. 构建数学模型,分析问题
问题一中,学生通过在平面直角坐标系中描点,可以直观地观察出描出的点都在一条直线上(如图2)。
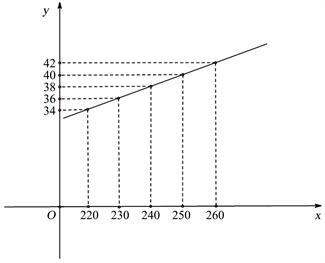
. plot points in the cartesian coordinate system
图2. 在平面直角坐标系中描点
教师加以引导,根据所学知识,学生能够判断并推测鞋号与脚长呈一次函数的关系。通过描绘对应点、观察直观的图像、思考推断鞋号与脚长的变化规律的过程,促进学生运用数学的思维思考我们的现实世界。
借来下进入问题二,通过问题一的观察分析,建立一次函数模型解决问题,设鞋号y与脚长x的关系的一般形式为:
根据已有的参数,任取两点,代入一般形式,解二元一次方程组即可求得函数解析式,完成模型的求解。
联立二元一次方程组:
解得:
所以得到鞋号y与脚长x的关系为:
作出函数图像后可以发现参数上所有的点都在此函数图像上,或者将参数点代入此函数中验算,都可以验证模型的正确性。
问题三属于模型的推广和应用,将脚长代入所得函数模型中,我们可以获得所需购买的鞋号。运动员的脚长为272 mm,代入模型求得鞋号为44.4。需要注意的是,不能盲目的四舍五入为44号,要联系生活实际,选鞋时宁可大一点也不可小一点,所以答案为该运动应选择45号鞋。
【设计意图】:学生基于数学的思维理解问题后,要建立鞋号与脚长的关系模型是教学的重点和难点,这一步也是培养学生会运用数学的语言表达我们的现实世界的关键。在教学中,以学生的自主探究、合作学习为主,教师引导学生摸索规律,解决问题,推广和应用结果,推动学生的素养的形成。
4.4. 解释拓展应用,解决问题
融入数学建模的综合与实践教学最后应该做好成果的总结和教学的拓展。成果的总结可以是项目报告书的形式,让学生从总结的过程中分析不足,温故而知新。同时要做好教学的拓展,一方面在教学结束时做好教学留白,抛出更深层次的问题,例如本文《鞋号问题》中脚长与鞋号在平面直角坐标系中的点是恰好在一条直线上,如果不在一条直线上又该如何解决问题呢?另一方面,教师可以利用数学软件,展示数学软件在数学建模中的强大应用,调动学生的学习兴趣,增长学生的见识。比如利用matlab软件编写函数拟合代码求解《鞋号问题》(如图3)。
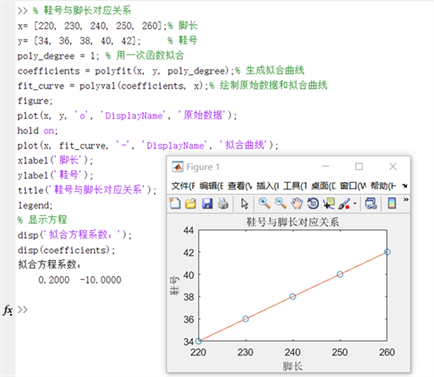
. the program and results obtained by solving with matlab
图3. 用matlab求解的程序及结果
5. 数学建模融入综合与实践教学的教学建议
5.1. 以教材为本——面向未来,培养跨学科学习能力
综合与实践教学的问题情境设计应该始于教材。必须根据学生已经掌握的知识,结合日常生活中存在的实际问题,才能激发学生运用所学知识主动解决实际问题的能力。在设计情境和问题时,需要提前考虑解决问题可能需要运用的知识。在数学建模活动中,通常会涉及一些学生尚未学习过的知识,部分学生尚未接触的知识是可以接受的。一方面,这有助于培养学生现学现用的能力;另一方面,未知的内容也能够激发学生的好奇心,提高学生的学习兴趣。然而,新知识的引入不宜过多,应以教材为基础。建构主义学习理论也强调,要使学生能够基于已有经验解决问题,从而使他们获得新的经验,以达到更好的学习效果。
5.2. 设置合适的难度——面对现实,培养综合实践能力
要根据中学生的认知发展水平合理地设置问题情境,对问题本身的难度要进行适当的调整。从中学生的认知发展水平看,处于形式运算阶段的中学生,思维具有一定的灵活性,但如果照搬数学建模竞赛的活动对于中学生来说,其难度系数过高,而且很难在短短的课堂中完成全部过程。这就要求教师根据学生的实际情况选择适宜的素材,设计适合学生参与的难度,让绝大多数学生都能参与其中。要做到这一点并不容易,需要教师在教学实践中不断地积累经验,并在反思中不断地总结规律。通过不断地教学实践,才能得出结论。提高学生解决问题的能力是一方面,最重要的是学生通过全程参与的过程中培养各方面综合素养。
5.3. 建立多样的评价体系——面向发展,聚焦核心素养
对于综合与实践教学的评价,应该注重评价方式的多样性、评价维度的多元性,评价主体的多样性和评价结果呈现的多样性。对于课程的教学评价,在评价方式上可以有活动课程观察、活动成果、课后访谈、成长记录等。评价维度应该包括“四基”“四能”的达成,尤其关注核心素养的表现等方面。评价主体可以包括教师、学生等,学生可以自评互评,通过自评、互评反思不足,汲取他人的优点而不断进步。评价的结果应定性定量结合呈现,例如对学生在活动的问题解决上进行分数制评分,活动中的各项表现采用等级制评分,两者有机结合形成评价结果。总之,综合与实践教学的评价要注重多元性、多样性和灵活性,避免过于主观的评价和“唯分数论”。
6. 结语
数学建模融入初中数学综合与实践教学,是按照新课标所提出的课程性质、理念、目标、内容及实施方式等方面的一种教学实施策略。这是一种以问题驱动的教学方式进行的教学,但是,它的驱动问题并没有一个统一的标准。它可以根据课程标准,结合学生的特征,参考当地文化特征,以及与时新热点的联系等方面,进行多元的、开放的设计,使学生能够在一个真实的环境中,去发现问题,去分析问题,去建立模型,去解决这个问题。由此使学生充分体会到数学是认知世界的思考工具、表达工具。此外,在教学过程中,教师可以运用信息技术来丰富学习内容,改善教学方式,并使学生的创造性思维得到发展,发挥新课标下教师作为学生学习引导者角色的作用,更好的实现对学生“三会”核心素质的培养。
致谢
感谢周昱老师对本篇论文的指导和帮助。
基金项目
吉首大学研究生校级科研项目(jdy22031)。